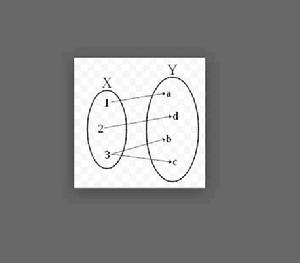
概述
多值函式定義:設X是一個非空數集,Y是非空數集 ,f是個對應法則 , 若在X中有至少一個元素x,按對應法則f,Y有至少兩個元素y與之對應,且對X中的所有元素x,按對應法則f,都有Y中的元素y與之對應,則稱f為從X到Y的多值函式,記作y=f(x)。
若對定義域每一個自變數x,其對應的函式值f(x)是唯一的,則稱f(x)是單值函式,反之則稱f(x)是多值函式。關鍵字“每一個”,“唯一的”。
單值函式定義:設X是一個非空數集,Y是非空數集 ,f是個對應法則 , 若對X中的每個x,按對應法則f,使Y中存在唯一的一個元素y與之對應 , 就稱對應法則f是X上的一個函式,記作y=f(x)。習慣上也說y是x的函式。
這兩個定義的區別可抓關鍵字的變化,“唯一的”變為“至少一個”且具備“一對多”的情況。
舉例
多值函式的例子:
(1)若│f(x)│=2x-1,則f(x)=±(2x-1),一個自變數x對應兩個函式值。
(2)y=sinx (x∈R)在R上的反函式(註:在單值函數裡,是"在[-π/2,π/2]上為多值函式)
(3)y=Arcsinx,一個自變數x對應無數個函式值。
(4)每個大於0的實數都有二個實數的平方根,例如4的平方根是{−2, +2}.,0的平方根是0。
(5)一般而言,許多不為0的複數都有二個平方根、三個立方根、n個n次方根,只有0的n次方根為0。
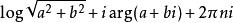 多值函式
多值函式(6)複對數函式是多值函式。log(a+bi)( a和b為實數)的值是,其中 n為任意整數。 .
(7)反三角函式為周期性的多值函式,例如
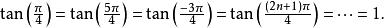 多值函式
多值函式因此,arctan(1)在本質上會對應許多數值:π/4, 5π/4, −3π/4等。若限制其tan x的定義域在−π/2 < x<π/2,此區域下tan x為單純遞增,則arctan( x)的值域會在−π/2 < y<π/2。這種限定區域下的值稱為主值。
(8)不定積分也可以視為是多值函式,函式 f的不定積分是一個函式的集合,集合中的每一個函式微分後都是 f,因此不定積分存在一積分常數,因為積分常數不論本身數值多少,微分後都是0。
(9)所有的多值函式都是來自非單射的函式,因為原始函式無法完全保存其輸入的資訊,因此函式也就不可逆。
(10)複變函數的多值函式會有分支點,例如n次方根以及對數函式中,0是分支點,而arctan函式中,虛數單位 i和− i為分支點。利用分支點可以限定範圍的方式,將這些函式重新定義為單值函式。若是在實函式的例子中,這個限制的區域一般會稱為函式的主分支。
相關問題
1、函式是指實數集對實數集的映射,而從映射的角度出發是定義域中的每個元素只能有一個像。多值函式的一個X可以有兩個Y與之對應,這是否與函式的定義相違背?
如果定義函式是映射的一種,那么從映射的定義上來看,多值函式不是函式。如果定義函式是一種對應法則(許多課本亦如此定義),那么毫無疑問,多值函式是函式的一類。
所以多值函式是不是函式取決於對於函式的定義。可以說狹義的函式特指單值函式,但是廣義的函式既包含單值函式,也包含多值函式。
你認為的矛盾是已經從某種意義上把多值函式歸為函式範疇了,如果你把術語函式換成對應來就好理解,對應和多值對應從字面意思就能看出他們所指並不一樣,所以並不存在矛不矛盾的話題。就相當於解釋什麼是‘維’‘一維’‘二維’‘多維’一樣。
2、多值函式是不是函式?
問題出在函式的定義里,在早些年出版的教材里,函式的定義里沒有“唯一”兩個字,因此函式就有單值函式與多值函式的區分,按那種定義,多值函式是函式;近些年出版的教材里,函式的定義里有“唯一”兩字,因此函式都是單值的,從這個意義上說,多值函式就不是函式了。