切線判定定理

切線判斷定理：經過半徑外端點並且垂直於這條半徑的直線是圓的切線。

切線的判定方法

【定義】

如果直線與圓只有一個公共點，這時直線

與圓的位置關係叫做相切。這條直線叫做圓的切線，這個公共點叫做切點。

切線性質：圓的切線垂直於經過切點的半徑。

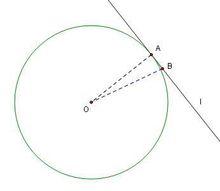切線判定定理

【證明】

已知：直線l與⊙O有交點A，且OA⊥l ；

求證：l是⊙O的切線。

證明：假設直線l不是⊙O的切線，

則⊙O與l有兩個交點，設另外一個交點為B，連線OB。

由於A、B都是⊙O上的點，因此OA=OB。又OA⊥l ，由於直角三角形中斜邊大於直角邊，

有OA<OB，與OA=OB矛盾；

因此假設不成立，l是⊙O的切線。