《高一數學》
高一數學（人教版）的知識掌握較多，高一試題約占高考得分的60%，一學年要學五本書，只要把高一的數學掌握牢靠，高二，高三則只是對高一的複習與補充。
基本信息
- 類別：數學教科書
- 出版社：人民教育出版社
- 性質：數學必修一
內容簡介
高一數學技巧要點整體把握是很重要的，高中數學的重要性不是誰能想像的，剛進入高一，有些學生還不是很適應，如果直接學習高考技巧仿佛是“沒學好走就想跑”。任何的技巧都是建立在牢牢的基礎知識之上，因此建議高一的學生多抓基礎，多看課本。在應試教育中，只有多記公式定理，掌握解題技巧，熟悉各種題型，才能在考試中取得最好的成績。在高考中只會做題是不行的，一定要在會的基礎上加個“熟練”才行，小題一般要控制在每個兩分鐘左右。集合及運算的概念集合：一般的，一定範圍內某些確定的，不同的對象的全體構成一個集合。子集：對於兩個集合A和B，如果集合A中的任意一個元素都是集合B中的元素，我們就說這兩個集合有包含關係，稱集合A是集合B的子集，記作A⊆B讀作A包含於B空集：不含任何元素的集合叫做空集。記為Φ集合的三要素：確定性、互異性、無序性集合的表示方法：列舉法、描述法、視圖法、區間法集合的分類：（按集合中元素個數多少分為：）有限集、無限集、空集常見數集“N”全體非負整數(或自然數）組成的集合“N+”或“N*”所有正整數組成的集合“Z”全體整數組成的集合"Q“全體有理數組成的集合“R”全體實數組成的集合關係：元素屬於集合：a∈A集合與集合：A⊇B，A=B運算：交集：由屬於集合A且屬於集合B的所有元素組成的集合，叫做集合A與集合B的交集。記作A∩B並集：由所有屬於集合A或屬於集合B的元素組成的集合，叫做集合A與B的並集記作A∪B補集：由全集U中不屬於集合A的所有元素組成的集合，記為CuA運算的基本性質集合的運算性質（1）A∩B=B∩A；A∩B⊆A；A∩B⊆B；A∩U=A；A∩A=A；A∩φ=φ；（2）A∪B=BUA；A⊆A∪B；B⊆A∪B；A∪U=U；A∪A=A；A∪φ=A；（3）Cu（CuA）=A；Cuφ=U；CuU=φ；A∩CuA=φ；A∪CuA=U（摩根定律或反演律）；（4）A⊇B，B⊇A，則A=B，A⊇B，B⊇C，則A⊇C常用結論(1)A⊆B<=>A∩B=A;A⊆B<=>A∪B=B;A∪B=A∩B<=>A=B(2)CuA∩CuB=Cu(A∪B)，CuA∪CuB=Cu(A∩B)——德摩根律有關公式
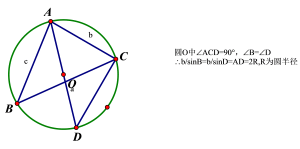
拋物線y=ax^2+bx+c就是y等於a乘x的平方加上bx再加上ca>0時開口向上a<0時開口向下c=0時拋物線經過原點b=0時拋物線對稱軸為y軸還有頂點式y=a（x-h)^2+k就是y等於a乘以（x-h）的平方+k-h是頂點坐標的xk是頂點坐標的y一般用於求最大值與最小值拋物線標準方程:y^2=2px它表示拋物線的交點在x的正半軸上,焦點坐標為(p/2,0)準線方程為x=-p/2由於拋物線的交點可在任意半軸,故共有標準方程y^2=2pxy^2=-2pxx^2=2pyx^2=-2py三角函式兩角和公式sin(A+B)=sinAcosB+cosAsinBsin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB)tan(A-B)=(tanA-tanB)/(1+tanAtanB)cot(A+B)=(cotAcotB-1)/(cotB+cotA)cot(A-B)=(cotAcotB+1)/(cotB-cotA)倍角公式tan2α=2tanα/(1-tan^2(α))sin2α=2sinαcosαcos2α=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α)sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*(n-1)/n]=0cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π*(n-1)/n]=0及sin^2(α)+sin^2(α-2π/3)+sin^2(α+2π/3)=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0萬能公式：sinα=2tan(α/2)/[1+tan^2(α/2)]cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]tanα=2tan(α/2)/[1-tan^2(α/2)]半角公式sin(A/2)=√((1-cosA)/2)cos(A/2)=√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA))cot(A/2)=√((1+cosA)/((1-cosA))和差化積2sinAcosB=sin(A+B)+sin(A-B)2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)+cos(A-B)-2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2cosA+cosB=2cos((A+B)/2)cos((A-B)/2)tanA+tanB=sin(A+B)/cosAcosBtanA-tanB=sin(A-B)/cosAcosBcotA+cotBsin(A+B)/sinAsinB-cotA+cotBsin(A+B)/sinAsinB某些數列前n項和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n-1)=n^22+4+6+8+10+12+14+…+(2n)=n(n+1)1^2+2^2+3^2+4^2+5^2+6^2+7^2+8^2+…+n^2=n(n+1)(2n+1)/61^3+2^3+3^3+4^3+5^3+6^3+…n^3=(n(n+1)/2)^21*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3正弦定理a/sinA=b/sinB=c/sinC=2R註：其中R表示三角形的外接圓半徑餘弦定理b^2=a^2+c^2-2accosB註：角B是邊a和邊c的夾角乘法與因式分解a^2-b^2=(a+b)(a-b),a^3+b^3=(a+b)(a^2-ab+b^2),a^3-b^3=(a-b(a^2+ab+b^2)三角不等式|a+b|≤|a|+|b||a-b|≤|a|+|b||a|≤b<=>-b≤a≤b|a-b|≥|a|-|b -|a|≤a≤|a|一元二次方程的解-b+√(b2-4ac)/2a-b-√(b2-4ac)/2a根與係數的關係x1+x2=-b/ax1*x2=c/a註：韋達定理判別式b2-4ac=0註：方程有相等的兩實根b2-4ac>0註：方程有兩個不相等的個實根b2-4ac<0註：方程有共軛複數根公式分類公式表達式圓的標準方程(x-a)2+(y-b)2=r2註：（a,b）是圓心坐標圓的一般方程x2+y2+Dx+Ey+F=0註：D2+E2-4F>0拋物線標準方程y2=2pxy2=-2pxx2=2pyx2=-2py直稜柱側面積S=c*h斜稜柱側面積S=c'*h正稜錐側面積S=1/2c*h'正稜台側面積S=1/2(c+c')h'圓台側面積S=1/2(c+c')l=pi(R+r)l球的表面積S=4pi*r2圓柱側面積S=c*h=2pi*h圓錐側面積S=1/2*c*l=pi*r*l弧長公式l=a*ra是圓心角的弧度數r>0扇形面積公式s=1/2*l*r錐體體積公式V=1/3*S*H圓錐體體積公式V=1/3*pi*r2h斜稜柱體積V=S'L註：其中,S'是直截面面積，L是側棱長柱體體積公式V=s*h圓柱體V=pi*r2h圖形周長面積體積公式長方形的周長=（長+寬）×2正方形的周長=邊長×4長方形的面積=長×寬正方形的面積=邊長×邊長三角形的面積已知三角形底a，高h，則S=ah/2已知三角形三邊a,b,c,半周長p,則S=√[p(p-a)(p-b)(p-c)]（海倫公式）（p=(a+b+c)/2）和：（a+b+c)*(a+b-c)*1/4已知三角形兩邊a,b,這兩邊夾角C，則S=absinC/2設三角形三邊分別為a、b、c，內切圓半徑為r則三角形面積=(a+b+c)r/2設三角形三邊分別為a、b、c，外接圓半徑為r則三角形面積=abc/4r已知三角形三邊a、b、c,則S=√{1/4[c^2a^2-((c^2+a^2-b^2)/2)^2]}(“三斜求積”南宋秦九韶）|ab1|S△=1/2*|cd1||ef1||ab1||cd1|為三階行列式,此三角形ABC在平面直角坐標系內A(a,b),B(c,d),C(e,f),這裡ABC|ef1|選區取最好按逆時針順序從右上角開始取，因為這樣取得出的結果一般都為正值，如果不按這個規則取，可能會得到負值，但不要緊，只要取絕對值就可以了，不會影響三角形面積的大小！秦九韶三角形中線面積公式:S=√[(Ma+Mb+Mc)*(Mb+Mc-Ma)*(Mc+Ma-Mb)*(Ma+Mb-Mc)]/3其中Ma,Mb,Mc為三角形的中線長.平行四邊形的面積=底×高梯形的面積=（上底+下底）×高÷2直徑=半徑×2半徑=直徑÷2圓的周長=圓周率×直徑=圓周率×半徑×2圓的面積=圓周率×半徑×半徑長方體的表面積=（長×寬+長×高+寬×高）×2長方體的體積=長×寬×高正方體的表面積=棱長×棱長×6正方體的體積=棱長×棱長×棱長圓柱的側面積=底面圓的周長×高圓柱的表面積=上下底面面積+側面積圓柱的體積=底面積×高圓錐的體積=底面積×高÷3長方體（正方體、圓柱體）的體積=底面積×高平面圖形名稱符號周長C和面積S正方形a—邊長C=4aS=a2長方形a和b－邊長C=2(a+b)S=ab三角形a,b,c－三邊長h－a邊上的高s－周長的一半A,B,C－內角其中s=(a+b+c)/2S=ah/2=ab/2?sinC=[s(s-a)(s-b)(s-c)]1/2=a2sinBsinC/(2sinA)有關定理
高一數學1過兩點有且只有一條直線2兩點之間線段最短3同角或等角的補角相等4同角或等角的餘角相等5在同一平面內，過一點有且只有一條直線和已知直線垂直6直線外一點與直線上各點連線的所有線段中，垂線段最短7平行公理，經過直線外一點，有且只有一條直線與這條直線平行8如果兩條直線都和第三條直線平行或垂直，這兩條直線也互相平行9同位角相等，兩直線平行10內錯角相等，兩直線平行11同旁內角互補，兩直線平行12兩直線平行，同位角相等13兩直線平行，內錯角相等14兩直線平行，同旁內角互補15定理，三角形兩邊的和大於第三邊16推論，三角形兩邊的差小於第三邊17三角形內角和定理，三角形三個內角的和等於180°18推論1，直角三角形的兩個銳角互餘19推論2，三角形的一個外角等於和它不相鄰的兩個內角的和20推論3，三角形的一個外角大於任何一個和它不相鄰的內角21全等三角形的對應邊、對應角相等22邊角邊公理(SAS)有兩邊和它們的夾角對應相等的兩個三角形全等23角邊角公理(ASA)有兩角和它們的夾邊對應相等的兩個三角形全等24推論(AAS)有兩角和其中一角的對邊對應相等的兩個三角形全等25邊邊邊公理(SSS)有三邊對應相等的兩個三角形全等26斜邊、直角邊公理(HL)有斜邊和一條直角邊對應相等的兩個直角三角形全等27定理1，在角的平分線上的點到這個角的兩邊的距離相等28定理2，到一個角的兩邊的距離相同的點，在這個角的平分線上29角的平分線是到角的兩邊距離相等的所有點的集合30等腰三角形的性質定理，等腰三角形的兩個底角相等(即等邊對等角）31推論1，等腰三角形頂角的平分線平分底邊並且垂直於底邊32等腰三角形的頂角平分線、底邊上的中線和底邊上的高互相重合33推論3，等邊三角形的各角都相等，並且每一個角都等於60°34等腰三角形的判定定理，如果一個三角形有兩個角相等，那么這兩個角所對的邊也相等（等角對等邊）35推論1，三個角都相等的三角形是等邊三角形36推論2，有一個角等於60°的等腰三角形是等邊三角形37在直角三角形中，如果一個銳角等於30°那么它所對的直角邊等於斜邊的一半38直角三角形斜邊上的中線等於斜邊上的一半39定理，線段垂直平分線上的點和這條線段兩個端點的距離相等40逆定理和一條線段兩個端點距離相等的點，在這條線段的垂直平分線上41線段的垂直平分線可看作和線段兩端點距離相等的所有點的集合42定理1，關於某條直線對稱的兩個圖形是全等形43定理2，如果兩個圖形關於某直線對稱，那么對稱軸是對應點連線的垂直平分線44定理3，兩個圖形關於某直線對稱，如果它們的對應線段或延長線相交，那么交點在對稱軸上45逆定理，如果兩個圖形的對應點連線被同一條直線垂直平分，那么這兩個圖形關於這條直線對稱46勾股定理，直角三角形兩直角邊a、b的平方和、等於斜邊c的平方，即a^2+b^2=c^247勾股定理的逆定理，如果三角形的三邊長a、b、c有關係a^2+b^2=c^2，那么這個三角形是直角三角形48定理，四邊形的內角和等於360°49四邊形的外角和等於360°50多邊形內角和定理，n邊形的內角的和等於（n-2）×180°51推論，任意多邊的外角和等於360°52平行四邊形性質定理1，平行四邊形的對角相等53平行四邊形性質定理2，平行四邊形的對邊相等54推論，夾在兩條平行線間的平行線段相等55平行四邊形性質定理3，平行四邊形的對角線互相平分56平行四邊形判定定理1，兩組對角分別相等的四邊形是平行四邊形57平行四邊形判定定理2，兩組對邊分別相等的四邊形是平行四邊形58平行四邊形判定定理3，對角線互相平分的四邊形是平行四邊形59平行四邊形判定定理4，一組對邊平行相等的四邊形是平行四邊形60矩形性質定理1，矩形的四個角都是直角61矩形性質定理2，矩形的對角線相等62矩形判定定理1，有三個角是直角的四邊形是矩形63矩形判定定理2，對角線相等的平行四邊形是矩形64菱形性質定理1，菱形的四條邊都相等65菱形性質定理2，菱形的對角線互相垂直，並且每一條對角線平分一組對角66菱形面積=對角線乘積的一半，即s=（a×b）÷267菱形判定定理1，四邊都相等的四邊形是菱形68菱形判定定理2，對角線互相垂直的平行四邊形是菱形69正方形性質定理1，正方形的四個角都是直角，四條邊都相等70正方形性質定理2，正方形的兩條對角線相等，並且互相垂直平分，每條對角線平分一組對角71定理1，關於中心對稱的兩個圖形是全等的72定理2，關於中心對稱的兩個圖形，對稱點連線都經過對稱中心，並且被對稱中心平分73逆定理，如果兩個圖形的對應點連線都經過某一點，並且被這一點平分，那么這兩個圖形關於這一點對稱74等腰梯形性質定理，等腰梯形在同一底上的兩個角相等75等腰梯形的兩條對角線相等76等腰梯形判定定理，在同一底上的兩個角相等的梯形是等腰梯形77對角線相等的梯形是等腰梯形78平行線等分線段定理，如果一組平行線在一條直線上截得的線段相等，那么在其他直線上截得的線段也相等79推論1，經過梯形一腰的中點與底平行的直線，必平分另一腰80推論2，經過三角形一邊的中點與另一邊平行的直線，必平分第三邊81三角形中位線定理，三角形的中位線平行於第三邊，並且等於它的一半82梯形中位線定理，梯形的中位線平行於兩底，並且等於兩底和的一半l=（a+b）÷2s=l×h83(1)比例的基本性質，如果a:b=c:d,那么ad=bc如果ad=bc,那么a:b=c:d84(2)合比性質，如果a/b=c/d,那么(a±b)/b=(c±d)/d85(3)等比性質，如果a/b=c/d=…=m/n(b+d+…+n≠0),那么(a+c+…+m)/(b+d+…+n)=a/b86平行線分線段成比例定理，三條平行線截兩條直線，所得的對應線段成比例87推論，平行於三角形一邊的直線截其他兩邊（或兩邊的延長線），所得的對應線段成比例88定理，如果一條直線截三角形的兩邊（或兩邊的延長線）所得的對應線段成比例，那么這條直線平行於三角形的第三邊89平行於三角形的一邊，並且和其他兩邊相交的直線，所截得的三角形的三邊與原三角形三邊對應成比例90定理，平行於三角形一邊的直線和其他兩邊（或兩邊的延長線）相交，所構成的三角形與原三角形相似91相似三角形判定定理1，兩角對應相等，兩三角形相似（asa）92直角三角形被斜邊上的高分成的兩個直角三角形和原三角形相似93判定定理2，兩邊對應成比例且夾角相等，兩三角形相似（sas）94判定定理3，三邊對應成比例，兩三角形相似（sss）95定理，如果一個直角三角形的斜邊和一條直角邊與另一個直角三角形的斜邊和一條直角邊對應成比例，那么這兩個直角三角形相似96性質定理1，相似三角形對應高的比，對應中線的比與對應角平分線的比都等於相似比97性質定理2，相似三角形周長的比等於相似比98性質定理3，相似三角形面積的比等於相似比的平方99任意銳角的正弦值等於它的餘角的餘弦值，任意銳角的餘弦值等於它的餘角的正弦值100任意銳角的正切值等於它的餘角的餘切值，任意銳角的餘切值等於它的餘角的正切值101圓是定點的距離等於定長的點的集合102圓的內部可以看作是圓心的距離小於半徑的點的集合103圓的外部可以看作是圓心的距離大於半徑的點的集合104同圓或等圓的半徑相等105到定點的距離等於定長的點的軌跡，是以定點為圓心，定長為半徑的圓106和已知線段兩個端點的距離相等的點的軌跡，是著條線段的垂直平分線107到已知角的兩邊距離相等的點的軌跡，是這個角的平分線108到兩條平行線距離相等的點的軌跡，是和這兩條平行線平行且距離相等的一條直線109定理，不在同一直線上的三點確定一個圓。110垂徑定理，垂直於弦的直徑平分這條弦並且平分弦所對的兩條弧111推論1，①平分弦（不是直徑）的直徑垂直於弦，並且平分弦所對的兩條弧②弦的垂直平分線經過圓心，並且平分弦所對的兩條弧③平分弦所對的一條弧的直徑，垂直平分弦，並且平分弦所對的另一條弧112推論2，圓的兩條平行弦所夾的弧相等113圓是以圓心為對稱中心的中心對稱圖形114定理，在同圓或等圓中，相等的圓心角所對的弧相等，所對的弦相等，所對的弦的弦心距相等115推論，在同圓或等圓中，如果兩個圓心角、兩條弧、兩條弦或兩弦的弦心距中有一組量相等那么它們所對應的其餘各組量都相等116定理，一條弧所對的圓周角等於它所對的圓心角的一半117推論1，同弧或等弧所對的圓周角相等；同圓或等圓中，相等的圓周角所對的弧也相等118推論2，半圓（或直徑）所對的圓周角是直角；90°的圓周角所對的弦是直徑119推論3，如果三角形一邊上的中線等於這邊的一半，那么這個三角形是直角三角形120定理，圓的內接四邊形的對角互補，並且任何一個外角都等於它的內對角121①直線l和⊙o相交d<r②直線l和⊙o相切d=r③直線l和⊙o相離d>r122切線的判定定理，經過半徑的外端並且垂直於這條半徑的直線是圓的切線123切線的性質定理，圓的切線垂直於經過切點的半徑124推論1，經過圓心且垂直於切線的直線必經過切點125推論2，經過切點且垂直於切線的直線必經過圓心126切線長定理，從圓外一點引圓的兩條切線，它們的切線長相等，圓心和這一點的連線平分兩條切線的夾角127圓的外切四邊形的兩組對邊的和相等128弦切角定理，弦切角等於它所夾的弧對的圓周角129推論，如果兩個弦切角所夾的弧相等，那么這兩個弦切角也相等130相交弦定理，圓內的兩條相交弦，被交點分成的兩條線段長的積相等131推論，如果弦與直徑垂直相交，那么弦的一半是它分直徑所成的兩條線段的比例中項132切割線定理，從圓外一點引圓的切線和割線，切線長是這點到割線與圓交點的兩條線段長的比例中項133推論，從圓外一點引圓的兩條割線，這一點到每條割線與圓的交點的兩條線段長的積相等134如果兩個圓相切，那么切點一定在連心線上135①兩圓外離，d>r+r②兩圓外切d=r+r③兩圓相交，r-r<d<r+r(r>r)④兩圓內切，d=r-r(r>r)⑤兩圓內含d<r-r(r>r)136定理，相交兩圓的連心線垂直平分兩圓的公共弦137定理，把圓分成n(n≥3):⑴依次連結各分點所得的多邊形是這個圓的內接正n邊形⑵經過各分點作圓的切線，以相鄰切線的交點為頂點的多邊形是這個圓的外切正n邊形138定理，任何正多邊形都有一個外接圓和一個內切圓，這兩個圓是同心圓139正n邊形的每個內角都等於（n-2）×180°/n140定理，正n邊形的半徑和邊心距把正n邊形分成2n個全等的直角三角形141正n邊形的面積sn=pnrn/2p表示正n邊形的周長142正三角形面積√3a²/4a表示邊長143如果在一個頂點周圍有k個正n邊形的角，由於這些角的和應為360°，因此k×(n-2)180°/n=360°化為（n-2）(k-2)=4144弧長計算公式：l=nπr/180145扇形面積公式：s扇形=nπr2/360=lr/2146內公切線長=d-(R-r)外公切線長=d-(r+r)147等腰三角形的兩個底角相等148等腰三角形的頂角平分線、底邊上的中線、底邊上的高相互重合三線合一149如果一個三角形的兩個角相等，那么這兩個角所對的邊也相等等邊對等角150三條邊都相等的三角形叫做等邊三角形函式知識點
函式1．函式的概念：設A、B是非空的數集，如果按照某個確定的對應關係f，使對於集合A中的任意一個數x，在集合B中都有唯一確定的數f(x)和它對應，那么就稱f：A→B為從集合A到集合B的一個函式．記作：y=f(x)，x∈A．其中，x叫做自變數，x的取值範圍A叫做函式的定義域；與x的值相對應的y值叫做函式值，函式值的集合{f(x)|x∈A}叫做函式的值域．注意：1．定義域：能使函式式有意義的實數x的集合稱為函式的定義域。求函式的定義域時列不等式組的主要依據是：(1)分式的分母不等於零；(2)偶次方根的被開方數不小於零；(3)對數式的真數必須大於零；(4)指數、對數式的底必須大於零且不等於1；(5)如果函式是由一些基本函式通過四則運算結合而成的。那么，它的定義域是使各部分都有意義的x的值組成的集合.(6)指數為零底不可以等於零，(7)實際問題中的函式的定義域還要保證實際問題有意義.。函式性質1.函式的單調性(局部性質)(1）增函式設函式y=f(x)的定義域為I，如果對於定義域I內的某個區間D內的任意兩個自變數x1，x2，當x1<x2時，都有f(x1)<f(x2)，那么就說f(x)在區間D上是增函式.區間D稱為y=f(x)的單調增區間.。如果對於區間D上的任意兩個自變數的值x1，x2，當x1<x2時，都有f(x1)>f(x2)，那么就說f(x)在這個區間上是減函式。區間D稱為y=f(x)的單調減區間。注意：函式的單調性是函式的局部性質。圖象的特點如果函式y=f(x)在某個區間是增函式或減函式，那么說函式y=f(x)在這一區間上具有(嚴格的)單調性，在單調區間上增函式的圖象從左到右是上升的，減函式的圖象從左到右是下降的。函式單調區間與單調性的判定方法(A)定義法：1任取x1，x2∈D，且x1<x2；2作差f(x1)－f(x2)；3變形（通常是因式分解和配方）；4定號（即判斷差f(x1)－f(x2)的正負）；5下結論（指出函式f(x)在給定的區間D上的單調性）。（B)圖象法(從圖象上看升降)(C)複合函式的單調性複合函式f[g(x)]的單調性與構成它的函式u=g(x)，y=f(u)的單調性密切相關，其規律：“同增異減”。注意：函式的單調區間只能是其定義域的子區間,不能把單調性相同的區間和在一起寫成其並集。資料；五年高考三年模擬