基本概述
切比雪夫不等式基本原理
對於任一隨機變數X,若EX與DX均存在,則對任意ε0,恆有P{|X-EX|=ε}=DX/ε^2或P{|X-EX|ε}=1-DX/ε^2，切比雪夫不等式說明，DX越小，則P{|X-EX|=ε}越小，P{|X-EX|ε}越大，也就是說，隨機變數X取值基本上集中在EX附近，這進一步說明了方差的意義。
同時當EX和DX已知時，切比雪夫不等式給出了機率P{|X-EX|=ε}的一個上界，該上界並不涉及隨機變數X的具體機率分布，而只與其方差DX和ε有關，因此，切比雪夫不等式在理論和實際中都有相當廣泛的套用。需要指出的是，雖然切比雪夫不等式套用廣泛，但在一個具體問題中，由它給出的機率上界通常比較保守。
切比雪夫不等式是指在任何數據集中，與平均數的距離超過K倍標準差的數據占的比例至多是1/K^2。
基本定義
在機率論中，切比雪夫不等式顯示了隨機變數的「幾乎所有」值都會「接近」平均。這個不等式以數量化這方式來描述，究竟「幾乎所有」是多少，「接近」又有多接近：
與平均相差2個標準差的值，數目不多於1/4
與平均相差3個標準差的值，數目不多於1/9
與平均相差4個標準差的值，數目不多於1/16
……
與平均相差k個標準差的值，數目不多於1/K^2
舉例說，若一班有36個學生，而在一次考試中，平均分是80分，標準差是10分，我們便可得出結論：少於50分（與平均相差3個標準差以上）的人，數目不多於4個（=36*1/9）。
測度論說法
設(X,Σ,μ)為一測度空間，f為定義在X上的廣義實值可測函式。對於任意實數t0，
一般而言，若g是非負廣義實值可測函式，在f的定義域非降，則有
上面的陳述，可透過以|f|取代f，再取如下定義而得：
機率論說法
設X為隨機變數，期望值為μ，方差為σ2。對於任何實數k0，
改進
一般而言，切比雪夫不等式給出的上界已無法改進。考慮下面例子：
這個分布的標準差σ=1/k，μ=0。
當只求其中一邊的值的時候，有Cantelli不等式。
基本證明
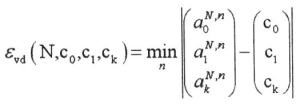切比雪夫不等式亦可從機率論的原理和定義開始證明。本文用現代機率論方法,證明馬爾可夫不等式與切比雪夫不等式,特別是給出兩個不等式等號成立的充要條件,這在流行的機率統計教科書中是沒有的.結果的證明主要依賴下面的引理.引理設Y是樣本空間)上的隨機變數,P(Y≥0)=1,則E(Y)=0若且唯若P(Y=0)=0.證明記IA為集合A的示性函式.若P(Y=0)=1,則P(Y40)=0,P(Y0)=0,於是,E(Y)=E(YI{Y40}YI{Y=0}YI{Y0})=000=0.反之,若P(Y≥0)=1,E(Y)=0,則必有P(Y=0)=1.否則,P(Y40)40,由機率的連續性及{Y40}=9∞n=1{Y41n},
得P(Y40)=limn:∞P(Y41n),因而存在n0∈\,P(Y41n0)40,E(Y)≥E(1n0I{Y41n0})=1n0P(Y41n0)40,與假設E(Y)=0矛盾.定理1(馬爾可夫(Markov)不等式)設Y是樣本空間)上的非負隨機變數且有有限期望,則;(40,P(Y≥()≤E(Y)(.其中等號成立若且唯若P(Y∈{0,(})=1.證明注意到I{Y≥(}≤Y(,兩邊取期望,由E(IA)=P(A),即得不等式成立.記Y=Y(-I{Y≥(},則Y≥0,P(Y≥0)=1.結論中等號成立等價於E(Y)=0,由引理,E(Y)=0等價於P(Y=0)=1,等價於P(Y=(I{Y≥(})=1,等價於P(Y∈{0,(})=1.證畢.定理2(切比雪夫(Chebyshev)不等式)設Y是樣本空間)上的隨機變數,有有限期望*和方差2。
