馬爾可夫不等式

在機率論中，馬爾可夫不等式給出了隨機變數的函式大於等於某正數的機率的上界。雖然它以俄國數學家安德雷·馬爾可夫命名，但該不等式曾出現在一些更早的文獻中，其中包括馬爾可夫的老師--巴夫尼提·列波維奇·切比雪夫。

基本信息

• 英文名：馬爾可夫不等式

• 過程：把機率關聯到數學期望
• 作用：給出了隨機變數的累積分布函式
• 表達式：P(|x|≥a)≤E(|X|)/a

簡介

馬爾可夫不等式把機率關聯到數學期望，給出了隨機變數的累積分布函式一個寬泛但仍有用的界。
馬爾可夫不等式的一個套用是，不超過1/5的人口會有超過5倍於人均收入的收入。

表達式

X為一非負隨機變數，則P(|x|≥a)≤E(|X|)/a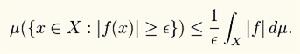

切比雪夫不等式

若用測度領域的術語來表示，馬爾可夫不等式可表示為若(X,Σ,μ)是一個測度空間，ƒ為可測的擴展實數的函式，且ε≥0，則μ({x∈X：|f(x)≥ε|})≤(1/ε)∫[x]|f|dμ
有時上述的不等式會被稱為切比雪夫不等式

推論

切比雪夫不等式使用變異數來作為一隨機變數超過平均值機率的上限，可以用下式表示：
Pr(|X-E(X)|≥a)≤Var(X)/a^2
對任意a>0，Var(X)為X的變異數，定義如下：
Var(X)=E[(X-E(X))^2]
若以馬爾可夫不等式為基礎，切比雪夫不等式可視為考慮隨機變數(X-E(X))^2
根據馬爾可夫不等式，可得到以下的結果
Pr((X-E(X))^2≥a^2)≤Var(X)/a^2

矩陣形式

令M≥0為自共軛矩陣形式的隨機變數，且a>0，則有右圖不等式

矩陣形式的馬爾可夫不等式

套用實例

馬爾可夫不等式可用來證明切比雪夫不等式。
馬爾可夫不等式可用來證明一個非負的隨機變數，其平均值和中位數滿足的關係。