簡介
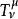 共形反常
共形反常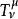 共形反常
共形反常共形反常是一種在量子化過程中出現的一個現象。以愛因斯坦場方程式的能動張量 為例,當有效作用量 經由重整化後,會產生一個正的量值和負的量值,其中物質能動張量的跡不為零,然而重整化前原本的量為零,這意味著原本的對稱關係被破壞,違反共形不變性,即為共形反常。共形反常在重整化後才物理意義,而引起物質能動張量反常的原因則為背景時空的非平直性。
重整化
重整化( Renormalization)是量子場論、場的統計力學和自相似幾何結構中解決計算過程中出現無窮大的一系列方法。
在量子場論發展的早期,人們發現許多圈圖(即微擾展開的高階項)的計算結果含有發散(即無窮大)項。重整化是解決這個困難的一個方案。一個理論如果只有有限種發散項,則可以在拉氏量中引進有限數目的項來抵消這些無窮大項,這種情形被稱為可重整。反之,如果理論中有無限種發散項,則稱為不可重整。
可重整化曾被認為一個場論所必需滿足的自洽性要求。它在量子電動力學和量子規範場論的發展過程中起過重要的作用。粒子物理的標準模型也是可重整的。
現代場論的觀點認為所有理論都只是有效理論,它們都有它們的適用範圍。除了所謂的終極理論,所有理論在原則上都是不可重整的。在這種觀點下,重整化只是聯繫不同能標下理論的一種方法。
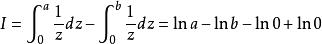 共形反常
共形反常例如: 的後兩項發散。
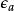 共形反常
共形反常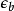 共形反常
共形反常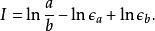 共形反常
共形反常為了消除發散,把積分下限分別改為無窮小的和,這樣積分就變成了
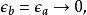 共形反常
共形反常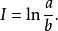 共形反常
共形反常如果能保證那么就可以得到
共形映射
數學上, 共形變換(英語:Conformal map)或稱 保角變換,來自於流體力學和幾何學的概念,是一個保持角度不變的映射。
更正式的說,一個映射
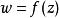 共形反常
共形反常 共形反常
共形反常 共形反常
共形反常稱為在 共形(或者 保角),如果它保持穿過的曲線間的定向角度,以及它們的取向也就是說方向。共形變換保持了角度以及無窮小物體的形狀,但是不一定保持它們的尺寸。
共形的性質可以用坐標變換的導數矩陣雅可比矩陣的術語來表述。如果變換的雅可比矩陣處處都是一個標量乘以一個旋轉矩陣,則變換是共形的。
參見
反常
