擬對稱映射

介紹

數學上，度量空間之間的 擬對稱映射，是雙利普希茨映射的一個推廣。雙利普希茨映射把一個集合的直徑擴大或縮小不超過某常數倍，而擬對稱映射就適合一個較弱的幾何性質，就是保持了集合的相對大小：如果集合 A和 B有直徑 t，其間距離不超過 t，那么這兩個集合的大小的比例改變不超過某常數倍。擬對稱映射和擬共形映射也有關係，因為在很多情況這兩者其實等價。

定義

設( X, d)和( Y, d)是度量空間。一個同胚 f: X→ Y稱為 η-擬對稱，若有一個遞增函式 η:[0,∞)→[0,∞)，使得對 X中任何三個不同的點 x, y, z都有

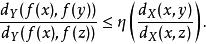擬對稱映射

基本性質

（1）逆映射是擬對稱的：

若 f: X→ Y是可逆 η-擬對稱映射，則其逆映射是 η-擬對稱，其中 η( t)=1/ η(1/ t).

（2）擬對稱映射保持集合的相對大小：

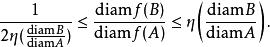擬對稱映射

若 A和 B是 X的子集， A是 B的子集，則