共形場論
共形場論、 保角場論( conformal field theory, CFT) 是量子場論一支,研究共形對稱之量子場組成之結構 (數學上或相通於處臨界點之統計力學模型) 。一此結構亦俗稱“一共形場論”。此論中最為人知者是二維共形場論,因其有一巨大、對應於各全純函式之無限維局部共形變換群。
共形場論有用於弦論、統計力學、凝態物理。
共形映射
數學上, 共形變換(英語:Conformal map)或稱 保角變換,來自於流體力學和幾何學的概念,是一個保持角度不變的映射。
更正式的說,一個映射
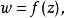 共形對稱
共形對稱 共形對稱
共形對稱 共形對稱
共形對稱稱為在 共形(或者 保角),如果它保持穿過的曲線間的定向角度,以及它們的取向也就是說方向。共形變換保持了角度以及無窮小物體的形狀,但是不一定保持它們的尺寸。
共形的性質可以用坐標變換的導數矩陣雅可比矩陣的術語來表述。如果變換的雅可比矩陣處處都是一個標量乘以一個旋轉矩陣,則變換是共形的。
製圖
在測繪學中,一個 共形變換投影是一個保持除有限點外所有點的角度不變的地圖投影。尺寸依賴於地點,但不依賴於方向。
其例子有麥卡托投影和極射投影。
複分析
共形映射很重要的一組例子來自複分析。若 U是一個複平面 C的開集,則一個函式 f: U→ C是共形的,若且唯若它在U上是一個全純函式,而且它的導數處處非零。若 f是一個反全純函式(也就是全純函式的復共軛),它也保持角度,但是它會將定向反轉。
黎曼映射定理是複分析最深刻的定理之一,它表明任何 C的單連通非空開子集上有一個到 C中的開單位圓盤的雙射。
參閱
•AdS/CFT對偶
•運算元積展開
•頂點代數
•WZW模型
•臨界點
•共形反常
