交換子群

在抽象代數中，一個群的換位子群或導群，是指由這個群的所有交換子所生成的子群，記作[G,G]、G′或G(1) 。每個群都對應著一個確定的交換子群。在一個群G的所有正規子群中，交換子群G′是使得G對它的商群為交換群的最小子群。在某種意義上，交換子群提供了群G的可交換程度。因為從交換子的定義：[x,y]= xyx^(-1)y^(-1) ，如果x與y交換，那么[x,y]=e。一個群內可交換的元素越多，交換子就越少，交換子群也就越小。可交換群的交換子群為平凡群e。

定義

給定一個群G，G的交換子群或導群：[G,G'] 、G'或者G(1) 是G的所有交換子所生成的子群：

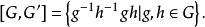交換子群

類似地可以定義高階的導群。

交換子群

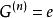交換子群

交換子群

可以證明，如果存在自然數n, 使得 ，那么G是可解群。

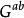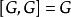交換子群

交換子群

商群 G/[G,G]是一個阿貝爾群，叫做 G的 阿貝爾化子群，通常記作 。 G的阿貝爾化子群就是 G的一階同調群。 的群叫做完美群，這是與阿貝爾群相對的概念。完美群的阿貝爾化子群是單位群{e}。

性質

G' 是G的正規子群;

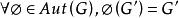交換子群

G對於自同構穩定： ;

如果H是G的子群， 那么H'屬於G';

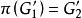交換子群

π:G1--> G2 是一個滿同態， 那么 ;

如果H是G的正規子群，那么G/H 是交換群，若且唯若G' 屬於H;

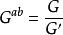交換子群

G’屬於G', 所以

套用

4次交替群的交換子群是克萊因四元群;

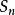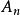交換子群

交換子群

n次對稱群 的交換子群是n次交替群 ;

四元群 Q= {1, −1, i, − i, j, − j, k, − k} 的交換子群是 {1, −1}。