倍角公式
二倍角
sin2α=2cosαsinα=2tanα/（1+tan²α）
cos2α=cos²α-sin²α=1-2sin²α=2cos²α－1
tan2α=2tanα/[1－(tanα)²][1]
二倍角變式
sin2α=sin^2(α+π/4)－cos^2(α+π/4)=2sin^2(a+π/4)－1=1－2cos^2(α+π/4);
cos2α=2sin(α+π/4)cos(α+π/4)
三倍角
sin3α=3sinα-4sin³α
cos3α=4cos³α-3cosα
tan3α=（3tanα-tan³α）/（1-3tan²α）
sin3α=4sinα×sin（π/3-α）sin（π/3+α）
cos3α=4cosα×cos（π/3-α）cos（π/3+α)
tan3α=tanα×tan（π/3-α）tan（π/3+α）
n倍角
根據歐拉公式(cosθ+i·sinθ)^n=cosnθ+i·sinnθ（註：sinθ前的i是虛數單位，即-1開方）
將左邊用二項式定理展開分別整理實部和虛部可以得到下面兩組公式
sin(nα)=ncos^(n-1)α·sinα-C(n,3)cos^(n-3)α·sin^3α+C(n,5)cos^(n-5)α·sin^5α-…
cos(nα)=cos^nα-C(n,2)cos^(n-2)α·sin^2α+C(n,4)cos^(n-4)α·sin^4α
輔助角
Asinα+Bcosα=√(A^2+B^2)sin[α+arctan(B/A)]
Asinα+Bcosα=√(A^2+B^2)cos[α-arctan(A/B)]
半角公式
sin(α/2)=±√[(1-cosα)/2]
cos(α/2)=±√[(1+cosα)/2]
tan(α/2)=±√[(1-sinα)/(1+sinα)]=cosα/(1+cosα)=(1-cosα)/sinα=cscα-cotα
cot(α/2)=±√[(1+cosα)/(1-cosα)]=(1+cosα)/sinα=sinα/(1-cosα)=cscα+cotα
sec(α/2)=±√[(2secα/(secα+1)]
csc(α/2)=±√[(2secα/(secα-1)]
半倍角
sin²（α/2）=（1-cosα）/2
cos²（α/2）=（1+cosα）/2
tan²（α/2）=（1-cosα）/（1+cosα）
tan（α/2）=sinα/（1+cosα）=（1-cosα）/sinα
半角變形
sin²（α/2）=（1-cosα）/2
sin(a/2）=√[（1-cosα）/2]（a/2在一、二象限）
或=-√[（1-cosα）/2]（a/2在三、四象限）
cos²（α/2）=（1+cosα）/2
cos(a/2）=√[（1+cosα）/2]（a/2在一、四象限）
或=-√[（1+cosα）/2]（a/2在二、三象限）
tan²（α/2）=（1-cosα）/（1+cosα）
tan（α/2）=sinα/（1+cosα）=（1-cosα）/sinα=√[（1-cosα）/（1+cosα）]（a/2在一、三象限）
或=-√[（1-cosα）/（1+cosα）]（a/2在二、四象限）。
誘導公式
sin（2kπ+α）=sinα
cos（2kπ+α）=cosα
tan（kπ+α）=tanα
cot（2kπ+α）=cotα
sec（2kπ+α）=secα
csc（2kπ+α）=cscα
sin（π+α）=－sinα
cos（π+α）=－cosα
tan（π+α）=tanα
cot（π+α）=cotα
sec(π+α)=-secα
csc(π+α)=-cscα
sin（－α）=－sinα
cos（－α）=cosα
tan（－α）=－tanα
cot（－α）=－cotα
sec(-α)=secα
csc(-α)=-cscα
sin（π－α）=sinα
cos（π－α）=-cosα
tan（π－α）=－tanα
cot（π－α）=－cotα
sec(π-α)=-secα
csc(π-α)=cscα
sin（α-π）=－sinα
cos（α-π）=－cosα
tan（α-π）=tanα
cot（α-π）=cotα
sec(α-π)=-secα
csc(α-π)=－cscα
sin（2π－α）=－sinα
cos（2π－α）=cosα
tan（2π－α）=－tanα
cot（2π－α）=－cotα
sec(2π-α)=secα
csc(2π-α)=-cscα
sin（π/2+α）=cosα
cos（π/2+α）=－sinα
tan（π/2+α）=－cotα
cot（π/2+α）=－tanα
sec(π/2+α)=-cscα
csc(π/2+α)=secα
sin（π/2－α）=cosα
cos（π/2－α）=sinα
tan（π/2－α）=cotα
cot（π/2－α）=tanα
sec(π/2-α)=cscα
csc(π/2-α)=secα
sin（3π/2+α）=－cosα
cos（3π/2+α）=sinα
tan（3π/2+α）=－cotα
cot（3π/2+α）=－tanα
sec(3π/2+α)=cscα
csc(3π/2+α)=-secα
sin（3π/2－α）=－cosα
cos（3π/2－α）=－sinα
tan（3π/2－α）=cotα
cot（3π/2－α）=tanα
sec(3π/2-α)=-cscα
csc(3π/2-α)=-secα
2cos²α-1=1-2sin²α
sin²a+cos²a=1
sina/cosa=tana。
恆等變形
tan(a+π/4）=(tana+1）/（1-tana)
tan(a-π/4）=(tana-1）/（1+tana)
asinx+bcosx=[√（a²+b²）]{[a/√（a²+b²）]sinx+[b/√（a²+b²）]cosx}=[√（a²+b²）]sin(x+y)【輔助角公式，其中tany=b/a，或者說sinx=b/[√（a²+b²）],cosx=a/[√（a²+b²）]】
設A，B，C是三角形的三個內角
tanA+tanB+tanC=tanAtanBtanC
cotAcotB+cotBcotC+cotCcotA=1
(cosA)^2+(cosB)^2+(cosC)^2+2cosAcosBcosC=1
sin2A+sin2B+sin2C=4sinAsinBsinC
sinA+sinB+sinC=4cos(A/2)cos(B/2)cos(C/2)。
萬能代換
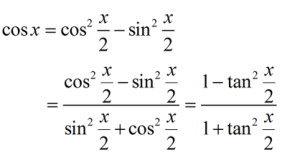三角恆等變換積化和差
sinα·cosβ=（1/2）[sin（α+β）+sin（α-β）]
cosα·sinβ=（1/2）[sin（α+β）-sin（α-β）]
cosα·cosβ=（1/2）[cos（α+β）+cos（α-β）]
sinα·sinβ=-（1/2）[cos（α+β）-cos（α-β）]（註：留意最前面是負號）。
內角公式
設A，B，C是三角形的三個內角
sinA+sinB+sinC=4cos（A/2）cos（B/2）cos（C/2）
cosA+cosB+cosC=1+4sin（A/2）sin（B/2）sin（C/2）
tanA+tanB+tanC=tanAtanBtanC
cot（A/2）+cot（B/2）+cot（C/2）=cot（A/2）cot（B/2）cot（C/2）
tan(A/2)tan(B/2)+tan(B/2)tan(C/2)+tan(C/2)tan(A/2)=1
cotAcotB+cotBcotC+cotCcotA=1
(cosA)^2+(cosB)^2+(cosC)^2+2cosAcosBcosC=1
sin2A+sin2B+sin2C=4sinAsinBsinC。
證明方法
三角恆等變換由此求得以上全部公式。
