三角形垂心

三角形垂心即三角形三邊高的交點。

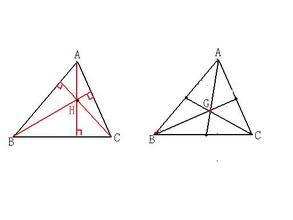
定義

垂心：三角形三邊高的交點

三角形垂心的性質

設�ABC的三條高為AD、BE、CF，其中D、E、F為垂足，垂心為H，角A、B、C的對邊分別為a、b、c，p=(a+b+c)/2．
1、銳角三角形的垂心在三角形內；直角三角形的垂心在直角頂點上；鈍角三角形的垂心在三角形外.
2、三角形的垂心是它垂足三角形的內心；或者說，三角形的內心是它旁心三角形的垂心；
3、 垂心H關於三邊的對稱點，均在△ABC的外接圓上。
4、 △ABC中，有六組四點共圓，有三組(每組四個)相似的直角三角形，且AH・HD=BH・HE=CH・HF。
5、 H、A、B、C四點中任一點是其餘三點為頂點的三角形的垂心(並稱這樣的四點為一―垂心組)。
6、 △ABC，△ABH，△BCH，△ACH的外接圓是等圓。
7、 在非直角三角形中，過H的直線交AB、AC所在直線分別於P、Q，則 AB/AP・tanB+

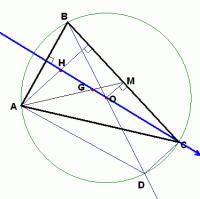三角形的垂心與外心的位置關係

AC/AQ・tanC=tanA+tanB+tanC。
8、 三角形任一頂點到垂心的距離，等於外心到對邊的距離的2倍。
9、 設O，H分別為△ABC的外心和垂心，則∠BAO=∠HAC，∠ABH=∠OBC，∠BCO=∠HCA。
10、 銳角三角形的垂心到三頂點的距離之和等於其內切圓與外接圓半徑之和的2倍。
11、 銳角三角形的垂心是垂足三角形的內心；銳角三角形的內接三角形(頂點在原三角形的邊上)中，以垂足三角形的周長最短。
12、
西姆松(Simson)定理（西姆松線）
從一點向三角形的三邊所引垂線的垂足共線的重要條件是該點落在三角形的外接圓上。
13、 設銳角�ABC內有一點T，那么T是垂心的充分必要條件是PB*PC*BC+PB*PA*AB+PA*PC*AC=AB*BC*CA。