銳角三角形:三個角都是銳角的三角形叫做銳角三角形。在直角三角形中，銳角A -百科知識中文網

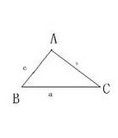
銳角三角形介紹

定義

三個角都是銳角的三角形叫做銳角三角形。

性質

1、大於0°而小於90°（直角）的角，叫做銳角。　

2、銳角三角形的三個角都是銳角（定義）。
3、設銳角三角形的三邊a c^2
4、銳角三角形的每條高均在三角形內。
5、三內角和180°。

銳角三角函式

定義

在直角三角形中，銳角A的對邊與斜邊的比叫做∠A的正弦；∠A的鄰邊與斜邊的比叫做∠A的餘弦；∠A的對邊與鄰居邊的比叫做∠A的正切。銳角A的正弦、餘弦、正切都叫做角A的 銳角三角函式（ trigonometric function of acute angle）。

銳角三角函式間的關係

sin (90°-a)=cos a, cos (90°-α)=sin α,
平方關係： sin^2 α+cos^2 α=1
倒數關係：cotα=(或tanα·cotα=1)

三角函式值

	30°	45°	60°
sin a	1/2	(√2)/2	(√3)/2
cos a	(√3)/2	(√2)/2	1/2
tan a	(√3)/3	1	√3

1、銳角三角函式值都是正值。
2、當角度在0°～90°間變化時，
正弦值隨著角度的增大（或減小）而增大（或減小）。
餘弦值隨著角度的增大（或減小）而減小（或增大）。
正切值隨著角度的增大（或減小）而增大（或減小）。

等邊三角形

定義

等邊三角形（ equilateral triangle），又稱正三角形，其三條邊長相等，且三個內角均為60°，是特殊的銳角三角形。

性質

（1）等邊三角形的內角都相等，且均為60°。
（2）等邊三角形每條邊上的中線、高線和所對角的平分線互相重合（三線合一）（3）等邊三角形是軸對稱圖形，它有三條對稱軸，對稱軸是每條邊上的中線、高線或對角的平分線所在的直線。
（4）等邊三角形重心、內心、外心、垂心重合於一點，稱為等邊三角形的中心。（四心合一）

等邊三角形的高

等邊三角形的高和其邊長的比為 √(3/4) ：1
證明：
作等邊三角形的一條高，將等邊三角形分為兩個全等的直角三角形，
設這個等邊三角形的邊長為a，則其中一個直角三角形一條直角邊長為1/2a，斜邊為a（即該等邊三角形. 由勾股定理，（直角三角形的兩直角邊的平方和等於斜邊的平方），得另一條直角邊（即該等邊三角形的高）為 √a^2-（1/2a)^2 = √(3/4a) ，即證.
由上，可推導出等邊三角形的面積公式：
S=1/2ah= （1/2）×[√(3/4a)] = [（√3）/4]×a^2

尺規作圖

可以利用尺規作圖的方式畫出正三角形，其作法相當簡單：先用尺畫出一條任意長度的線段（這條線段的長度決定等邊三角形的邊長），
等邊三角形的尺規作圖
再分別以線段二端點為圓心、線段為半徑畫圓，二圓匯交於二點，任選一點，和原來線段的兩個端點畫線段，則這二條線段和原來線段即構成一正三角形。

銳角三角形

基本信息