Euclid算法概述
歷史上第一個稱得上算法的好像就是這個歐幾里得算法,其實就是地球人都知道
的輾轉相除,故又叫“輾轉相除法”不要小看她,她是很美的。
簡單的描述就是,記gcd(a,b)表示非負整數a,b的最大公因數,那么:gcd(a,b)
=gcd(b,a%b)
Euclid算法定義
gcd(a,b)=gcd(b, a+kb) a,b,k為任意整數
即gcd(a,b)=gcd(b, a mod b) a≥0,b>0
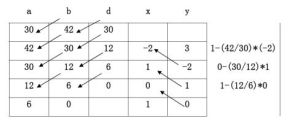
· Example:gcd(55,22)=gcd(22, 55mod22)=gcd(22,11)=11
證明:假定d=gcd(a,b),那么有d|a和d|b.對任何正整數b,a
可表示為如下形式: a=kb+r ≡r mod b, a mod b =r , 因
此,有(a mod b )= a-kb,k為某個整數。但由於d|b,b也
能整除kb, 而d|a,故有d|(a mod b), 這表明d 也是b 和(a
mod b) 的公因子。由於這是可逆的,如果d 是b 和(a mod
b) 的公因子,那么d|kb,且d|[kb+(a mod b)],這等同於
d|a。這樣a和b的公因子集合等同於b 和(a mod b) 的公因
子集合。
C語言的Euclid算法描述
//no matter a is bigger or b
//you should call anyone of them below
//non-recursion
unsigned int gcd(unsigned int a,unsigned int b){
int r;
while(b>0)
{
r=a%b;
a=b;
b=r;
}
return a;
}
//non-recursion
unsigned int gcd(unsigned int a,unsigned int b)
{
while(b^=a^=b^=a%=b);
return a;
}
//recursion
unsigned int gcd(unsigned int a,unsigned int b)
{
return (b>0)?gcd(b,a%b):a;
}
RSA中Euclid算法的套用
例題及分析
求兩個數的最大公約數gcd(55,22)=gcd(22, 55mod22)=gcd(22,11)=11
最常用的就是在RSA裡邊求密鑰
RSA算法,是非對稱加密的標準算法,其實算法很簡單:
找到兩個素數p,q,再找一個數r,使gcd(r,(p-1)(q-1))=1,也就是說互素,然後再找一個數m,使rm=1(mod (p-1)(q-1)),然後再作乘法n=pq,然後把pq丟掉,最好是讓任何人都不知道,包括自己(免得說夢話的時候被人聽到),然後手裡拿到r,m,n,r就是Private Key,只有你知道,而m,n就是Public Key。設信息為a,加密過程:a^m=b (mod n),b就是密文,解密過程:b^r=a(mod n),反過來用m加密,用r解密是一樣的。
Euclid算法的具體實現
#include
#include
#include
int mul(int x,int r,int n);//大樹冪乘
int niyuan(int n,int u); //求逆元
int gcd(int a,int b);//求最大公約數
bool IsPrime(int a );//判斷是否為素數
void main()
{
system("color 3f");
system("title ☆★ RSA公鑰密碼 ★☆");
cout<<"\t\t****RSA公鑰密碼加密解密系統****"<
int p ,q ;
cout<<" 請輸入兩個素數 :p , q :"<
cin>>p>>q;
int n=p*q;
int w=(p-1)*(q-1);
int e;
cout<<"請輸入加密密鑰 e (與"<<<"最大公約數為 1 )"<
cin>>e;
int d;
d=niyuan(w,e);
cout<<"經計算解密得到密鑰 :"<<
cout<<"輸入需要加密的明文:"<
int ming;
cin>>ming;
cout<<"經加密後得到的密文:"<<
cout<<"退出系統請按 1 "<
cout<<"進行解密請按 2 "<
int k;
cin>>k;
if(k==2)
{
cout<<"請輸入需解密的密文:"<
int miwen;
cin>>miwen;
cout<<"經解密後得到的明文:"<<
}
}
int mul(int x,int r,int n)//大樹冪乘函式
{
int a=x;
int b=r;
int c=1;
while(b!=0)
{
if(b%2!=0)
{
b=b-1;
c=(c*a)%n;
}
else
{
b=b/2;
a=(a*a)%n;
}
}
return c ;
}
int niyuan(int n,int u)//求逆元
{
int n1=n;
int n2=u;
int b1=0;
int b2=1;
int q=n1/n2;
int r=n1-q*n2;
while(r!=0)
{
n1=n2;
n2=r;
int t=b2;
b2=b1-q*b2;
b1=t;
q=n1/n2;
r=n1-q*n2;
}
if(n2!=1)
{
return 0 ;
}
else
{
return (b2+n)%n;
}
}
int gcd(int a,int b)//求最大公約數
{
int n1=a;
int n2=b;
int q=n1/n2;
int r=n1-q*n2;
while(r!=0)
{
n1=n2;
n2=r;
q=n1/n2;
r=n1-q*n2;
}
return n2 ;
}
bool IsPrime(int a)//判斷是否為素數
{
int b=(int)sqrt(a);
for(int i=2;i<=b;i++)
{
if (a%i==0)
return true;
}
return false;
}