概念
高斯線定理:四邊形ABCD中,直線DA與直線CB交於K,直線BA與直線CD交於L,N、M分別為AC、BD的中點,NM交KL與P.則P是KL中點
 高斯線定理
高斯線定理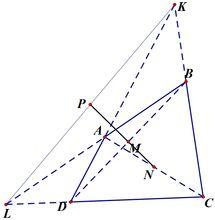 高斯線定理
高斯線定理證明
面積證法
由共邊比例定理知
KP/LP=KMN面積/LMN面積 (1)由定比分點公式的補充公式,得
KMN面積=1/2(KMC面積-KMA面積)
LMN面積=1/2(LMA面積-LMC面積) (2)
由BM=MD=1/2*BD,得
KMC面積=1/2*KDC面積,KMA面積=1/2*KBA面積
LMA面積=1/2*LDA面積,LMC面積=1/2*LBC面積 (3)
(3)代入(2),得
KMN面積=1/4*(KDC面積-KBA面積)=1/4*ABCD面積
LMN面積=1/4*ABCD面積
代入(1),得到KP=LP
平行四邊形證法
作AR,MK,BN平行於LC,AS,DP,LK平行於KC
根據平行四邊形對角線的性質S四邊形ASRC=S四邊形LMAP=S四邊形JQAN
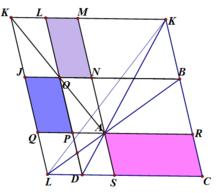 高斯線定理
高斯線定理∴S四邊形JQAP=S四邊形LONM
∴A在四邊形KMAQ的對角線KA中,A,O,K三點共線
則AC,CO,CK的中點三點共線
則由平行四邊形得對角線互相平分所以SR,,BD,KL三點的中點也共線
證畢
補充定理:
1.所謂的平行四邊形對角線的性質就是如果過平行四邊形對角線的一點分別作兩邊的平行線,則不含這條對角線的兩平行四邊形面積相等(如下圖)
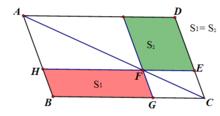 高斯線定理
高斯線定理2.三角形中位線性質:直線AB外有一點P則P與AB線上點的連線的中點都共線
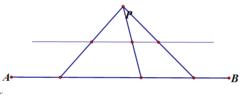 高斯線定理
高斯線定理
