概念
散度定理是指在向量分析中,一個把向量場通過曲面的流動(即通量)與曲面內部的向量場的表現聯繫起來的定理。更加精確地說,散度定理說明向量場穿過曲面的通量,等於散度在曲面圍起來的體積上的積分。直觀地,所有源點的和減去所有匯點的和,就是流出這區域的淨流量。
高斯公式在工程數學中是一個很重要的結果,特別是靜電學和流體力學。
在物理和工程中,散度定理通常運用在三維空間中。然而,它可以推廣到任意維數。在一維,它等價於微積分基本定理;在二維,它等價于格林公式。
這個定理是更一般的斯托克斯公式的特殊情形。
定理
設空間閉區域Ω是由分片光滑的閉曲面Σ所圍起來的三維區域,函式 P( x, y, z)、 Q( x, y, z)、 R( x, y, z)在Ω上具有一階連續偏導數,則有
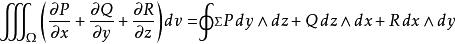 散度定理
散度定理或
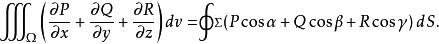 散度定理
散度定理這裡Σ是Ω的邊界(boundary),cos α、cos β、cos γ是Σ在點( x, y, z)處的單位法向量的方向餘弦。
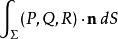 散度定理
散度定理 散度定理
散度定理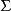 散度定理
散度定理這兩個公式都叫做 高斯公式,不過這兩公式僅僅是表達方式不同,其實是相同的定理,這可以用變數變換得到兩公式的右邊都等於 ,其中 是曲面 的向外單位法向量 。
表示方法
用散度表示
高斯公式用散度表示為:
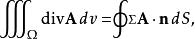 散度定理
散度定理 散度定理
散度定理其中Σ是空間閉區域Ω的邊界曲面,而 是曲面Σ上的朝外的單位法向量。
用向量表示
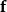 散度定理
散度定理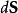 散度定理
散度定理令 V代表有一間單閉曲面 S為邊界的體積, 是定義在 V中和 S上連續可微的向量場。如果 是外法向向量面元,則
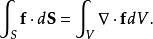 散度定理
散度定理推論
•對於標量函式g和向量場F的積,套用高斯公式可得:
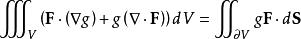 散度定理
散度定理•對於兩個向量場{\displaystyle \mathbf {F} \times \mathbf {G} }的向量積,套用高斯公式可得:
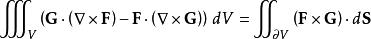 散度定理
散度定理•對於標量函式f和非零常向量的積,套用高斯公式可得:
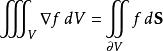 散度定理
散度定理•對於向量場F和非零常向量的向量積,套用高斯公式可得:
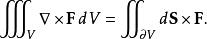 散度定理
散度定理例子
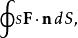 散度定理
散度定理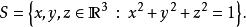 散度定理
散度定理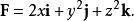 散度定理
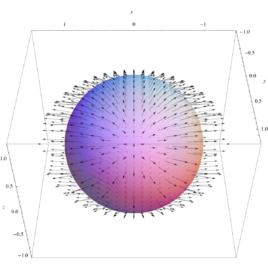
散度定理假設我們想要計算 其中S是一個單位球面,定義為 F是向量場:
直接計算這個積分是相當困難的,但我們可以用高斯公式來把它簡化:
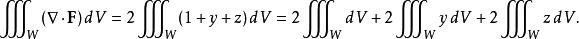 散度定理
散度定理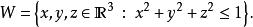 散度定理
散度定理其中W是單位球:
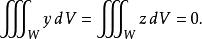 散度定理
散度定理由於函式y和z是奇函式,我們有:
因此:
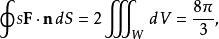 散度定理
散度定理因為單位球W的體積是4 π3.
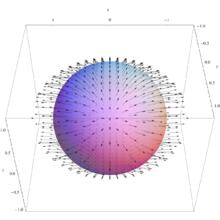 圖1.例題中向量場
圖1.例題中向量場說明:例子所對應的向量場。注意,向量可能指向球面的內側或者外側。
二階張量的散度定理
二階張量的高斯公式實際上是上面的高斯公式的推論。為了使內容完整,首先簡要地介紹三維歐幾里得空間上的 二階張量(詳見並矢張量或張量積)以及相關的概念和記號 。在這裡,向量和向量場用 黑斜體字母表示,張量用 正黑體字母表示。
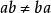 散度定理
散度定理1)兩個向量 a和 b並排放在一起所形成的量 ab被稱為向量 a和 b的 並矢或 並矢張量。注意,一般來說.
2)ab=0的充分必要條件是 a=0或 b=0。
3)二階張量就是 有限個並矢的線性組合。
4)ab分別線性地依賴於 a和 b。
5)二階張量 T和向量 a的縮並 T*a以及 a*T對, T和 a都是線性的。
6)特別是,當 T=uv時,
 散度定理
散度定理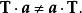 散度定理
散度定理所以,一般來說,。
定理:
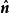 散度定理
散度定理 散度定理
散度定理 散度定理
散度定理設 V是三維歐幾里得空間中的一個有限區域,S是它的邊界曲面, 是S的外法線方向上的單位向量, T是定義在 V的某個開鄰域上 的連續的二階張量場, 是 T的轉置,則
 散度定理
散度定理