概述
高斯投影：它是一種橫軸等角切圓柱投影。高斯-克呂格簡介
高斯-克呂格(Gauss-Kruger)投影簡稱“高斯投影”，又名"等角橫切橢圓柱投影”，地球橢球面和平面間正形投影的一種。德國數學家、物理學家、天文學家高斯（CarlFriedrichＧauss，1777一1855）於十九世紀二十年代擬定，後經德國大地測量學家克呂格（JohannesKruger，1857～1928）於1912年對投影公式加以補充，故名。該投影按照投影帶中央子午線投影為直線且長度不變和赤道投影為直線的條件，確定函式的形式，從而得到高斯一克呂格投影公式。投影后，除中央子午線和赤道為直線外，其他子午線均為對稱於中央子午線的曲線。構想用一個橢圓柱橫切於橢球面上投影帶的中央子午線，按上述投影條件，將中央子午線兩側一定經差範圍內的橢球面正形投影於橢圓柱面。將橢圓柱面沿過南北極的母線剪開展平，即為高斯投影平面。取中央子午線與赤道交點的投影為原點，中央子午線的投影為縱坐標x軸，赤道的投影為橫坐標y軸，構成高斯克呂格平面直角坐標系。
高斯-克呂格特性
等角投影——投影前後的角度相等，但長度和面積有變形；
等距投影——投影前後的長度相等，但角度和面積有變形；
等積投影——投影前後的面積相等，但角度和長度有變形
高斯投影的基本概念
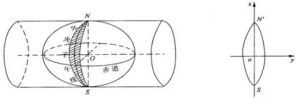高斯投影它是一種橫軸等角切圓柱投影。它把地球視為球體,假想一個平面捲成一個橫圓柱面並把它套在球體外面,使橫軸圓柱的軸心通過球的中心,球面上一根子午線與橫軸圓柱面相切。這樣,該子午線在圓柱面上的投影為一直線,赤道面與圓柱面的交線是一條與該子午線投影垂直的直線。將橫圓柱面展開成平面,由這兩條正交直線就構成高斯-克呂格平面直角坐標系。為減少投影變形,高斯-克呂格投影分為3o帶和6o帶投影。
測量學基礎
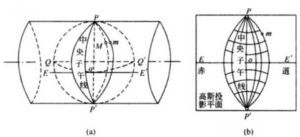高斯投影高斯投影分帶
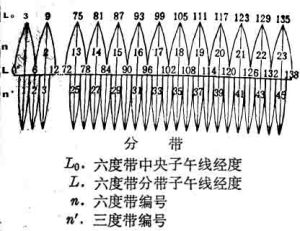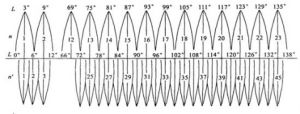
高斯投影分帶按一定經差將地球橢球面劃分成若干投影帶,這是高斯投影中限制長度變形的最有效方法。分帶時既要控制長度變形使其不大於測圖誤差，又要使帶數不致過多以減少換帶計算工作，據此原則將地球橢球面沿子午線劃分成經差相等的瓜瓣形地帶,以便分帶投影。通常按經差6度或3度分為六度帶或三度帶。六度帶自0度子午線起每隔經差6度自西向東分帶，帶號依次編為第1、2…60帶。三度帶是在六度帶的基礎上分成的，它的中央子午線與六度帶的中央子午線和分帶子午線重合，即自1.5度子午線起每隔經差3度自西向東分帶，帶號依次編為三度帶第1、2…120帶。我國的經度範圍西起73度東至135度，可分成六度帶十一帶或三度帶二十二帶。六度帶可用於中小比例尺（1：25000以下）測圖，三度帶可用於大比例尺（如1：10000）測圖。在某些特殊情況下，高斯投影也可採用寬頻或窄帶，如按經差9度或1.5度分帶。
高斯平面直角坐標系
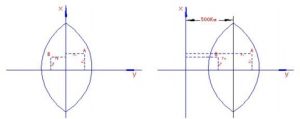高斯平面直角坐標系在投影面上，中央子午線和赤道的投影都是直線，並且以中央子午線和赤道的交點o作為坐標原點，以中央子午線的投影為縱坐標x軸，以赤道的投影為橫坐標y軸。
在我國坐標都是正的，坐標的最大值（在赤道上）約為330km。為了避免出現負的橫坐標，可在橫坐標上加上500000m。此外還應在坐標前面再冠以帶號。這種坐標稱為國家統一坐標。
這也就是為什麼在RTK測量中在輸入投影參數時，Y坐標加常數增加了500000m的原因。
高斯平面投影的特點
【1】中央子午線無變形【2】無角度變形，圖形保持相似
【3】離中央子午線越遠，變形越大
由此可見，在測量中，如果中央子午線輸錯了，投影的中央子午線就會偏離實地坐標系正確的中央子午線，變形就越大，最終的結果就使用測量的誤差更大。
中央子午線判斷方法
RTK使用中中央子午線的判斷
1、查看當地的經度
新到一個測區，如果別人只提供了坐標系而沒有提供中央子午線時，我們可以通過以下方式來判斷。
架設好儀器，在手薄中點擊下圖中右上角的“TG”快捷鍵，或按手薄上的“6”，或是點擊螢幕下方的“望遠鏡”圖示即可查看到當地的經緯度信息。
2、判斷當地的央央子午線
【1】引用國家控制點一般情況下國家控制點都是按正常的3度帶和6度帶。一般看坐標的帶號即可知道。在一般的RTK測量中，都是以3度帶來投影，這樣變形越小。根據之前所說L=3n來判斷中央子午線。
以經驗來計算，如上圖所示，選用經度中的度去除以3，如果不能整除時，往後減1得到112，往後加1得到114，再分別去除以3，如果能除盡，則說明此為中央子午線。在這裡114可以除盡，說明114為中央子午線，而它的控制範圍為左右1度30分，即112度30分~115度30分。而當前的113度21分在這個範圍內，說明114即為當地3度帶的中央子午線。
有時測區正好在兩個帶交叉的地方可是在某一帶的邊緣，這時在選擇已知點時一定要注意，不要同時使用兩個度帶中的已知點坐標進行求取轉換參數，必須使用時先進行度帶的換算。
由於大部分城市坐標係為了保密或是提高當地的精度，都是在原有的國家坐標繫上進行了平移鏇轉等參數的改變，所以設定坐標系橢球參數時選擇“用戶自定義”，輸入當前坐標系的“橢球系長軸”和“橢球系扁率，中央子午線也必須已知。個人無法判斷。
【3】自定義獨立坐標系在某些測量中，不加入國家已知點或城市坐標系的已知點，在設定投影參數時，可以延用54或80坐標系。根據測區的大小，在測區中心差不多位置查看一下當地的經度，假如：113度21分59.7601秒，在一般情況下投影到分上即可。在這裡我們就選用113度20分作為此測區的中央子午線。在RTK手薄中輸入“113.2”。
高斯簡介
物理學家、數學家卡爾•弗里德里希•高斯高斯（JohannCarlFriedrichGauss）（1777年4月30日—1855年2月23日），生於不倫瑞克，卒於哥廷根，德國著名數學家、物理學家、天文學家、大地測量學家。
高斯的成就遍及數學的各個領域，在數論、非歐幾何、微分幾何、超幾何級數、複變函數論以及橢圓函式論等方面均有開創性貢獻。他十分注重數學的套用，並且在對天文學、大地測量學和磁學的研究中也偏重於用數學方法進行研究。
高斯高斯雖然幼時家境貧困，但聰敏異常，受一貴族資助進學校受教育。1795～1798年在哥廷根大學學習，1798年轉入黑爾姆施泰特大學，翌年因證明代數基本定理獲博士學位。從1807年起擔任哥廷根大學教授兼哥廷根天文台台長直至逝世。
1792年，15歲的高斯進入Braunschweig學院。在那裡，高斯開始對高等數學作研究。獨立發現了二項式定理的一般形式、數論上的“二次互反律”(LawofQuadraticReciprocity)、“質數分布定理”(primenumertheorem)、及“算術幾何平均”(arithmetic-geometricmean)。
1795年高斯進入哥廷根大學。1796年，19歲的高斯得到了一個數學史上極重要的結果，就是《正十七邊形尺規作圖之理論與方法》。5年以後，高斯又證明了形如"Fermat素數"邊數的正多邊形可以由尺規作出。
1855年2月23日清晨，高斯於睡夢中去世。
