頻譜分析方法建模

頻譜分析方法建模，利用對頻譜（頻率的函式）的分析建立系統數學模型的方法，也就是根據系統對激勵信號(又稱輸入信號)的回響（又稱輸出信號）按頻率域內的分布規律來建模。線上性系統的情況下，根據輸入信號的傅立葉變換和輸出信號的傅立葉變換可以得到系統的傳遞函式。

頻譜分析方法建模

正文

利用對頻譜（頻率的函式）的分析建立系統數學模型的方法，也就是根據系統對激勵信號(又稱輸入信號)的回響（又稱輸出信號）按頻率域內的分布規律來建模。線上性系統的情況下，根據輸入信號的傅立葉變換和輸出信號的傅立葉變換可以得到系統的傳遞函式。利用不同頻率的正弦信號進行激勵並測量系統的回響，是建立系統傳遞函式模型的一種常用方法。譜分析方法所用的激勵信號是具有從零到某一最大頻率範圍內的寬頻信號，很便於測量，而且符合系統的實際運行狀態。這種激勵信號通常可通過純粹隨機過程（或某種瞬變過程）產生，因為它的能量在頻率域內分布較寬，可以對系統的回響同時作較全面的測量。如果系統是定常的和穩定的，則在隨機信號作用下的輸出也是隨機過程。根據維納的廣義諧波分析理論，一個平穩隨機過程x(t)的譜表達式為傅立葉-斯梯爾吉斯積分，即,這裡t表示時間，&owega;表示頻率，z(&owega;)為正交過程(不同&owega;處dz(&owega;)的協方差為零)。簡單地說,上式是把x(t)分解為具有隨機振幅|dz(&owega;)|和隨機相位arg dz(&owega;)的正弦函式之和。
在時間域中表達系統的輸出回響隨時間變化的關係時必須同時考慮當時輸入和既往輸入的全部影響，因此需要採用卷積運算。但在頻率域內表達輸出回響和輸入作用之間的關係比較簡單，如果以u（t）表示輸入，以y(t)表示輸出，並假設有與輸入無關的噪聲n(t)疊加在輸出端，則根據與頻率回響類似的道理有

式中φ(&owega;) 就是系統的傳遞函式。這個關係可以看作是的線性回歸。利用統計學方法可以得出φ(&owega;)的最小二乘估計是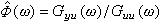

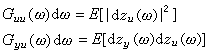
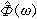式中Gyu(ω)是y(t)和u(t)的互譜,Guu(ω)是u(t)的自譜或功率譜。它們滿足關係式：

工程上常用適當方法對系統輸入寬頻帶激勵信號，然後記錄輸入和輸出過程，經過計算處理得到Gyu(ω)和Guu(ω)的估計（為減小估計方差，常用總體平均的方法處理）,從而求出的曲線。用某種函式，例如&owega; 的有理函式，在有效的頻率範圍內逼近上述函式，便可得到傳遞函式的數學模型。
傳遞函式表示u(t)和y(t)之間的線性關係，而噪聲和系統的非線性因素都會削弱這種關係。表征u（t）和y(t)間線性相依程度的頻率函式是相干函式，它的表達式為

並可解釋為輸出功率中歸因於輸入的部分在總的輸出功率中所占的比率。如果在任何頻率處r2呏1,則線性關係是嚴格的，否則r2就有可能小於 1。
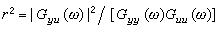
對於非平穩的情況（例如系統是時變的），則一般要引入時變頻譜，以描述每一瞬時不同頻率的功率分布。對於非線性模型的理論，在一般情況下要用無限多個頻率函式來描述非線性關係。工程上較為實用的是一些特定形式的非線性模型。
頻譜分析建模方法融合了傳統的傅立葉變換技術、統計估值理論、系統辨識和計算技術等方面的知識和成果，它的套用領域涉及地球物理、雷達、聲吶、圖像識別、語音識別、振動模態、海洋資源勘探、生物醫學和生態系統等各個方面。

配圖

相關連線