模態分析介紹
振動模態是彈性結構固有的、整體的特性。通過模態分析方法搞清楚了結構物在某一易受影響的頻率範圍內的各階主要模態的特性,就可以預言結構在此頻段內在外部或內部各種振源作用下產生的實際振動回響。因此,模態分析是結構動態設計及設備故障診斷的重要方法。
機器、建築物、航天航空飛行器、船舶、汽車等的實際振動模態各不相同。模態分析提供了研究各類振動特性的一條有效途徑。首先,將結構物在靜止狀態下進行人為激振,通過測量激振力與回響並進行雙通道快速傅立葉變換(FFT)分析,得到任意兩點之間的機械導納函式(傳遞函式)。用模態分析理論通過對試驗導納函式的曲線擬合,識別出結構物的模態參數,從而建立起結構物的模態模型。根據模態疊加原理,在已知各種載荷時間歷程的情況下,就可以預言結構物的實際振動的回響歷程或回響譜。
近十多年來,由於計算機技術、FFT分析儀、高速數據採集系統以及振動感測器、激勵器等技術的發展,試驗模態分析得到了很快的發展,受到了機械、電力、建築、水利、航空、航天等許多產業部門的高度重視。已有多種檔次、各種原理的模態分析硬體與軟體問世。
詳細說明
經典定義
模態分析的經典定義:將線性定常系統振動微分方程組中的物理坐標變換為模態坐標,使方程組解耦,成為一組以模態坐標及模態參數描述的獨立方程,以便求出系統的模態參數。坐標變換的變換矩陣為模態矩陣,其每列為模態振型。
用處
模態分析的最終目標是識別出系統的模態參數,為結構系統的振動特性分析、振動故障診斷和預報以及結構動力特性的最佳化設計提供依據。
模態分析技術的套用可歸結為以下幾個方面:
1) 評價現有結構系統的動態特性;
2) 在新產品設計中進行結構動態特性的預估和最佳化設計;
3) 診斷及預報結構系統的故障;
4) 控制結構的輻射噪聲;
5) 識別結構系統的載荷。
最佳懸掛點
模態試驗時,一般希望將懸掛點選擇在振幅較小的位置,最佳懸掛點應該是某階振型的節點。
最佳激勵點
最佳激勵點視待測試的振型而定,若單階,則應選擇最大振幅點,若多階,則激勵點處各階的振幅都不小於某一值。如果是需要許多能量才能激勵的結構,可以考慮多選擇幾個激勵點。
最佳測試點
模態試驗時測試點所得到的信息要求有儘可能高的信噪比,因此測試點不應該靠近節點。在最佳測試點位置其ADDOF(Average Driving DOF Displacement)值應該較大,一般可用EI(Effective Independance)法確定最佳測試點。
模態參數
模態參數有:模態頻率、模態振型、模態質量、模態向量、模態剛度和模態阻尼等。
主模態主空間主坐標
無阻尼系統的各階模態稱為主模態,各階模態向量所張成的空間稱為主空間,其相應的模態坐標稱為主坐標。
模態截斷
理想的情況下我們希望得到一個結構的完整的模態集,實際套用中這既不可能也不必要。實際上並非所有的模態對回響的貢獻都是相同的。對低頻回響來說,高階模態的影響較小。對實際結構而言,我們感興趣的往往是它的前幾階或十幾階模態,更高的模態常常被捨棄。這樣儘管會造成一點誤差,但頻響函式的矩陣階數會大大減小,使工作量大為減小。這種處理方法稱為模態截斷。
實模態和復模態
按照模態參數(主要指模態頻率及模態向量)是實數還是複數,模態可以分為實模態和復模態。對於無阻尼或比例阻尼振動系統,其各點的振動相位差為零或180度,其模態係數是實數,此時為實模態;對於非比例阻尼振動系統,各點除了振幅不同外相位差也不一定為零或180度,這樣模態係數就是複數,即形成復模態。
有限元分析
1)利用有限元分析模型確定模態試驗的測量點、激勵點、支持點(懸掛點),參照計算振型對測試模態參數進行辯識命名,尤其是對於複雜結構很重要。
2)利用試驗結果對有限元分析模型進行修改,以達到行業標準或國家標準要求。
3)利用有限元模型對試驗條件所產生的誤差進行仿真分析,如邊界條件模擬、附加質量、附加剛度所帶來的誤差及其消除。
4)兩套模型頻譜一致性和振型相關性分析。
5)利用有限元模型仿真分析解決實驗中出現的問題!
修正有限元分析的結果
用試驗模態分析的結果怎么修正有限元分析的結果?
1)結構設計參數的修正,可用最佳化方法進行。
2)子結構校正因子修正。
3)結構矩陣元素修正,包括非零元素和全元素修正兩種。
4)剛度矩陣和質量矩陣同時修正
過程
(1)動態數據的採集及頻響函式或脈衝回響函式分析
1)激勵方法。試驗模態分析是人為地對結構物施加一定動態激勵,採集各點的振動回響信號及激振力信號,根據力及回響信號,用各種參數識別方法獲取模態參數。激勵方法不同,相應識別方法也不同。目前主要由單輸入單輸出(SISO)、單輸入多輸出(SIMO)多輸入多輸出(MIMO)三種方法。以輸入力的信號特徵還可分為正弦慢掃描、正弦快掃描、穩態隨機(包括白噪聲、寬頻噪聲或偽隨機)、瞬態激勵(包括隨機脈衝激勵)等。
2)數據採集。SISO方法要求同時高速採集輸入與輸出兩個點的信號,用不斷移動激勵點位置或回響點位置的辦法取得振形數據。SIMO及MIMO的方法則要求大量通道數據的高速並行採集,因此要求大量的振動測量感測器或激振器,試驗成本較高。
3)時域或頻域信號處理。例如譜分析、傳遞函式估計、脈衝回響測量以及濾波、相關分析等。
(2)建立結構數學模型 根據已知條件,建立一種描述結構狀態及特性的模型,作為計算及識別參數依據。目前一般假定系統為線性的。由於採用的識別方法不同,也分為頻域建模和時域建模。根據阻尼特性及頻率耦合程度分為實模態或復模態模型等。
(3)參數識別 按識別域的不同可分為頻域法、時域法和混合域法,後者是指在時域識別復特徵值,再回到頻域中識別振型,激勵方式不同(SISO、SIMO、MIMO),相應的參數識別方法也不盡相同。並非越複雜的方法識別的結果越可靠。 對於目前能夠進行的大多數不是十分複雜的結構,只要取得了可靠的頻響數據,即使用較簡單的識別方法也可能獲得良好的模態參數;反之,即使用最複雜的數學模型、最高級的擬合方法,如果頻響測量數據不可靠,則識別的結果一定不會理想。
(4)振形動畫 參數識別的結果得到了結構的模態參數模型,即一組固有頻率、模態阻尼以及相應各階模態的振形。由於結構複雜,由許多自由度組成的振形也相當複雜,必須採用動畫的方法,將放大了的振形疊加到原始的幾何形狀上。
以上四個步驟是模態試驗及分析的主要過程。而支持這個過程的除了激振拾振裝置、雙通道FFT分析儀、台式或攜帶型計算機等硬體外,還要有一個完善的模態分析軟體包。通用的模態分析軟體包必須適合各種結構物的幾何物征,設定多種坐標系,劃分多個子結構,具有多種擬合方法,並能將結構的模態振動在螢幕上三維實時動畫顯示。
2.結構動力修改與靈敏度分析
結構動力修改(Structure Dynamic Modify——SDM)有兩個含義:①如果機器作了某種設計上的修改,它的動力學特性將會有何種變化?這個問題被稱為SDM的正問題。②如果要求結構動力學參數作某種改變,應該對設計作何種修改?這是SDM的反問題。
上述兩個問題,如果局限在有限元計算模型內解決,其正問題是比較簡單的,即只要改變參數重新計算一次就可以。其反問題就是特徵值的反問題,由於結構的複雜性和數學處理的難度較大,目前在理論上還不完善。只有涉及雅可比矩陣的問題得到了比較完善的解決,相應的力學模型是彈簧質量單向串聯繫統或桿件經過有限元或差分法離散的系統。此外,特徵值反問題的解決要求未修改系統計算的特徵值及特徵向量是精確的。因此,現在通常所指的SDM是指在試驗模態分析基礎上的。
不論是結構動力修改的正問題還是反問題,都要涉及針對結構進行修改。為了避免修改的盲目性,人們自然要問,如何修改才是最見成效的?換而言之,對一個機械系統,是進行質量修改,還是進行剛度修改?質量或剛度修改時,在機械結構上何處修改才是最靈敏部位,使得以較少的修改量得到較大的收穫?由此,引出了結構動力修改中的靈敏度分析技術。目前較為常見的是基於攝動的靈敏度分析。
模態分析技術從20世紀60年代後期發展至今已趨成熟,它和有限元分析技術一起成為結構動力學的兩大支柱。模態分析作為一種“逆問題”分析方法,是建立在實驗基礎上的,採用實驗與理論相結合的方法來處理工程中的振動問題。
實例解釋
 模態分析
模態分析 簡單地說,模態分析是根據用結構的固有特徵,包括頻率、阻尼和模態振型,這些動力學屬性去描述結構的過程。那只是一句總結性的語言,現在讓我來解釋模態分析到底是怎樣的一個過程。不涉及太多的技術方面的知識,我經常用一塊平板的振動模式來簡單地解釋模態分析。這個解釋過程對於那些振動和模態分析的新手們通常是有用的。
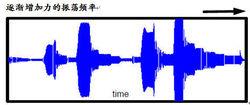
考慮自由支撐的平板,在平板的一角施加一個常力,由靜力學可知,一個靜態力會引起平板的某種靜態變形。但是在這兒我要施加的是一個以正弦方式變化,且頻率固定的振盪常力。改變此力的振動頻率,但是力的峰值保持不變,僅僅是改變力的振動頻率。同時在平板另一個角點安裝一個加速度感測器,測量由此激勵力引起的平板回響。
 模態分析
模態分析 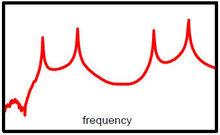 模態分析
模態分析 現在如果我們測量平板的回響,會注意到平板的回響幅值隨著激勵力的振動頻率的變化而變化。隨著時間的推進,回響幅值在不同的頻率處有增也有減。這似乎很怪異,因為我們對此系統僅施加了一個常力,而回響幅值的變化卻依賴於激勵力的振動頻率。具體到現在,當我們施加的激勵力的振動頻率越來越接近系統的固有頻率(或者共振頻率)時,回響幅值會越來越大,在激勵力的振動頻率等於系統的共振頻率時達到最大值。想想看,真令人大為驚奇,因為施加的外力峰值始終相同,而僅僅是改變其振動頻率。
時域數據提供了非常有用的信息,但是如果用快速傅立葉變換(FFT)將時域數據轉換到頻域,可以計算出所謂的頻響函式(FRF)。這個函式有一些非常有趣的信息值得關註:注意到頻響函式的峰值出現在系統的共振頻率處,注意到頻響函式的這些峰出現在觀測到的時域回響信號的幅值達到最大時刻的頻率處。
 模態分析
模態分析 如果我們將頻響函式疊加在時域波形之上,會發現時域波形幅值達到最大值時的激勵力振動頻率等於頻響函式峰值處的頻率。因此可以看出,既可以使用時域信號確定系統的固有頻率,也可以使用頻響函式確定這些固有頻率。顯然,頻響函式更易於估計系統的固有頻率。許多人驚奇結構怎么會有這些固有特徵,而更讓人驚奇的是在不同的固有頻率處,結構呈現的變形模式也不同,且這些變形模式依賴於激勵力的頻率。
 模態分析
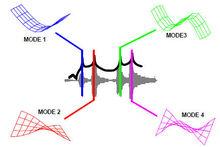
模態分析 現在讓我們了解結構在每一個固有頻率處的變形模式。在平板上均勻分布45個加速度計,用於測量平板在不同激勵頻率下的回響幅值。如果激勵力在結構的每一個固有頻率處駐留,會發現結構本身存在特定的變形模式。這個特徵表明激勵頻率與系統的某一階固有頻率相等時,會導致結構產生相應的變形模式。我們注意到當激勵頻率在第一階固有頻率處駐留時,平板發生了第1階彎曲變形,在圖中用藍色表示。在第2階固有頻率處駐留時,平板發生了第2階扭轉變形,在圖中用紅色表示。分別在結構的第3和第4階固有頻率處駐留時,平板發生了第3階彎曲變形,在圖中用綠色表示,和第4階扭轉變形,在圖中用紅紫紅色表示。這些變形模式稱為結構的模態振型。(從純數學角度講,這種叫法實際上不完全正確,但在這兒作為簡單的討論,從實際套用角度講,這些變形模式非常接近模態振型。)
我們設計的所有結構都具有各自的固有頻率和模態振型。本質上,這些特性取決於確定結構固有頻率和模態振型的結構質量和剛度分布。作為一名設計工程師,需要識別這些頻率,並且當有外力激勵結構時,應知道它們怎樣影響結構的回響。理解模態振型和結構怎樣振動有助於設計工程師設計更優的結構。模態分析有太多的需要講解的地方,但這個例子僅僅是一個非常簡單的解釋。現在我們能更好地理解模態分析主要是研究結構的固有特性。理解固有頻率和模態振型(依賴結構的質量和剛度分布)有助於設計噪聲和振動套用方面的結構系統。我們使用模態分析有助於設計所有類型的結構,包括機車、太空飛行器,宇宙飛船、計算機、網球拍、高爾夫球桿……這些清單舉不勝舉。
結構模態分析
模態向量有一個很重要的特性,即“模態正交性'”。所謂模態分析法,就是利用系統固有的模態的正交性,以系統的各階模態向量所組成的模態矩陣作為交換矩陣,對通常選取的物理坐標進行線性變換,使得振動系統以物理坐標和物理參數所描述、互相禍合的運動方程組,能夠變為一組彼此獨立的方程,每個獨立方程只含一個獨立的模態坐標。這個用模態坐標和模態參數所描述的各個獨立方程,稱為模態方程。模態分析實質上是一種坐標變換,其目的是為了解除方程的禍合,便於求解由於坐標變換是線性變換,因而系統在原有的物理系統中,對於任意激勵的回響,便可視為系統各階模態的線性組合,故模態分析法,又稱模態疊加法。而各階模態在疊加中所占的比重或加權係數,則取決於各階的模態坐標回響`。一般來說,高階模態比低階模態的加權係數要小得多,通常只需要選取前階模態進行疊加,即可達到足夠的精度。由此可知模態分析的主要優點就在於,它能用較少的運動方程或自由度數,直觀、簡明而又相當精確的去反映一個比較複雜結構的動態特性,從而大大減小測量、分析及計算的工作量。
基本假設
線性假設
假設被實驗識別系統是線性的,其物理意義是,結構系統對任一組同時作用的激勵的回響是該組內每一激勵單獨作用時系統的回響的線性疊加。基於這一個假設,我們有可能在實驗室內對系統施加容易實現、便於測量的作用力進行激勵,並由此提取被測系統的特徵參數,而不必施加與工作環境相同的激勵。
時不變假設
系統是定常的,即系統特徵參數為常量,滿足該假設的系統稱之為定常系統。例如,假設系統某特徵參數與溫度有關,則當溫度隨時間變化時,系統的特徵參數也隨之變化,則系統不滿足時不變假設,稱這樣的系統為非時不變系統。如果系統為非時不變系統,那么在不同時刻所測實驗數據將不一致,從而得不到穩定的系統特徵參數。
可觀測性
對於系統輸入、輸出的量測量結果應含有足夠的信息,以描述該系統適當特性的模型,否則稱該系統為不可觀測系統。此外還常常假設結構遵從互異性原理,即在點輸入所引起的點的回響,等於在點的相同輸入所引起的點的回響。此假設使得質量矩陣、剛度矩陣、阻尼矩陣和頻響函式矩陣都成了對稱矩陣。

