dfs[深度優先搜尋]

深度優先搜尋是一種在開發爬蟲早期使用較多的方法。它的目的是要達到被搜尋結構的葉結點(即那些不包含任何超鏈的HTML檔案) 。在一個HTML檔案中，當一個超鏈被選擇後，被連結的HTML檔案將執行深度優先搜尋，即在搜尋其餘的超鏈結果之前必須先完整地搜尋單獨的一條鏈。深度優先搜尋沿著HTML檔案上的超鏈走到不能再深入為止，然後返回到某一個HTML檔案，再繼續選擇該HTML檔案中的其他超鏈。當不再有其他超鏈可選擇時，說明搜尋已經結束。

基本信息

• 中文名：深度優先搜尋
• 英文名：Depth-First-Search

• 提出者：霍普克洛夫特與羅伯特·塔揚
• 套用學科：計算機

詳細解釋

事實上，深度優先搜尋屬於圖算法的一種，英文縮寫為DFS即Depth First Search.其過程簡要來說是對每一個可能的分支路徑深入到不能再深入為止，而且每個節點只能訪問一次.

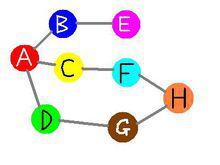圖

舉例說明之：下圖是一個無向圖，如果我們從A點發起深度優先搜尋（以下的訪問次序並不是唯一的，第二個點既可以是B也可以是C,D），則我們可能得到如下的一個訪問過程：A->B->E（沒有路了！回溯到A)->C->F->H->G->D（沒有路，最終回溯到A,A也沒有未訪問的相鄰節點，本次搜尋結束）.簡要說明深度優先搜尋的特點：每次深度優先搜尋的結果必然是圖的一個連通分量.深度優先搜尋可以從多點發起.如果將每個節點在深度優先搜尋過程中的"結束時間"排序（具體做法是創建一個list，然後在每個節點的相鄰節點都已被訪問的情況下，將該節點加入list結尾，然後逆轉整個鍊表)，則我們可以得到所謂的"拓撲排序",即topological sort.

基本思路

深度優先遍歷圖的方法是，從圖中某頂點v出發：

（1）訪問頂點v；

（2）依次從v的未被訪問的鄰接點出發，對圖進行深度優先遍歷；直至圖中和v有路徑相通的頂點都被訪問；

（3）若此時圖中尚有頂點未被訪問，則從一個未被訪問的頂點出發，重新進行深度優先遍歷，直到圖中所有頂點均被訪問過為止。　當然，當人們剛剛掌握深度優先搜尋的時候常常用它來走迷宮.事實上我們還有別的方法，那就是廣度優先搜尋(BFS).

窮舉

在我們遇到的一些問題當中，有些問題我們不能夠確切的找出數學模型，即找不出一種直接求解的方法，解決這一類問題，我們一般採用搜尋的方法解決。搜尋就是用問題的所有可能去試探，按照一定的順序、規則，不斷去試探，直到找到問題的解，試完了也沒有找到解，那就是無解，試探時一定要試探完所有的情況（實際上就是窮舉）；

對於問題的第一個狀態，叫初始狀態，要求的狀態叫目標狀態。

搜尋就是把規則套用於實始狀態，在其產生的狀態中，直到得到一個目標狀態為止。

產生新的狀態的過程叫擴展（由一個狀態，套用規則，產生新狀態的過程）

搜尋的要點：（1）初始狀態；

（2）重複產生新狀態；

（3）檢查新狀態是否為目標，是結束，否轉（2）；

如果搜尋是以接近起始狀態的程式依次擴展狀態的，叫寬度優先搜尋。

如果擴展是首先擴展新產生的狀態，則叫深度優先搜尋。

深度優先搜尋

深度優先搜尋用一個數組存放產生的所有狀態。

（1） 把初始狀態放入數組中，設為當前狀態；

（2） 擴展當前的狀態，產生一個新的狀態放入數組中，同時把新產生的狀態設為當前狀態；

（3） 判斷當前狀態是否和前面的重複，如果重複則回到上一個狀態，產生它的另一狀態；

（4） 判斷當前狀態是否為目標狀態，如果是目標，則找到一個解答，結束算法。

（5） 如果數組為空，說明無解。

對於pascal語言來講，它支持遞歸，在遞歸時可以自動實現回溯（利用局部變數）所以使用遞歸編寫深度優先搜尋程式相對簡單，當然也有非遞歸實現的算法。

搜尋是人工智慧中的一種基本方法，是一項非常普遍使用的算法策略，能夠解決許許多多的常見問題，在某些情況下我們很難想到高效的解法時，搜尋往往是可選的唯一選擇。按照標準的話來講：搜尋算法是利用計算機的高性能來有目的的窮舉一個問題的部分或所有的可能情況，從而求出問題的解的一種方法。

搜尋雖然簡單易學易於理解，但要掌握好並寫出速度快效率高最佳化好的程式卻又相當困難，總而言之，搜尋算法靈活多變，一般的框架很容易寫出，但合適的最佳化卻要根據實際情況來確定。在搜尋算法中，深度優先搜尋（也可以稱為回溯法）是搜尋算法里最簡單也最常見的，今天我們就從這裡講起，下面的內容假設讀者已經知道最基本的程式設計和簡單的遞歸算法。

系統算法

所有的搜尋算法從其最終的算法實現上來看，都可以劃分成兩個部分──控制結構和產生系統。正如前面所說的，搜尋算法簡而言之就是窮舉所有可能情況並找到合適的答案，所以最基本的問題就是羅列出所有可能的情況，這其實就是一種產生式系統。

我們將所要解答的問題劃分成若干個階段或者步驟，當一個階段計算完畢，下面往往有多種可選選擇，所有的選擇共同組成了問題的解空間，對搜尋算法而言，將所有的階段或步驟畫出來就類似是樹的結構（如圖）。

從根開始計算，到找到位於某個節點的解，回溯法（深度優先搜尋）作為最基本的搜尋算法，其採用了一種“一隻向下走，走不通就掉頭”的思想（體會“回溯”二字），相當於採用了先根遍歷的方法來構造搜尋樹。

上面的話可能難於理解，沒關係，我們通過基本框架和例子來闡述這個算法，你會發現其中的原理非常簡單自然。

基本框架

·dfs(狀態)

–if 狀態 是 目標狀態then

·dosomething

–else

·for 每個新狀態

–if 新狀態合法

»dfs(新狀態)

·主程式：

·dfs(初始狀態)

C++的實現

定義一個結構體來表達一個NODE的結構：

那么我們在搜尋一個樹的時候，從一個節點開始，能首先獲取的是它的兩個子節點。 例如：

A是第一個訪問的，然後順序是B和D、然後是E。然後再是C、F、G。那么我們怎么來保證這個順序呢？

這裡就應該用堆疊的結構，因為堆疊是一個先進後出的順序。通過使用C++的STL，下面的程式能幫助理解：

舉例

這道題來舉例（迷宮）

1	1	1	1
0	1	0	1
0	1	0	1
0	1	1	1

記錄起點為（1,1）找到所有的到（4,4）的路徑.

pascal程式如下：

這個程式的意思就是：進行搜尋一條路，直到不能走為止，換另一條路。