歷史發展
古希臘
古希臘畢達哥拉斯是初等數論的先驅。他與他的學派致力於一些特殊整數(如親和數、完全數、多邊形數)及特殊不定方程的研究。公元前4世紀,歐幾里德的《幾何原本》通過102個命題,初步建立了整數的整除理論。他關於“素數有無窮多個”的證明,被認為是數學證明的典範。
初等數論已經有2000年的歷史,公元前300年,歐幾里得發現了素數是數論的基石,他自己證明了有無窮多個素數。公元前250年古希臘數學家埃拉托塞尼發明了一種篩法。2000年來,數論學的一個最重要的任務,就是尋找一個可以表示所有素數的統一公式,或者稱為素數普遍公式,為此,人類耗費了巨大的心血。後來發現埃拉托塞尼篩法可以轉換成為一個素數產生的公式:
公元前250年同樣是古希臘的數學家埃拉托塞尼提出一種篩法:
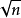 初等數論
初等數論(一)“要得到不大於某個自然數n(不等於0)的所有素數,只要在2至n中將不大於
的素數的倍數全部划去即可”。
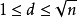 初等數論
初等數論(二)將上面的內容等價轉換:“如果n是合數(非0自然數),則它有一個因子d滿足
”。
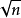 初等數論
初等數論(三)再從(二)得到等價的逆否命題:“若自然數n不能被不大於
的任何素數整除,則n是一個素數”。
(四)上述的(三)可以用符號如此表達:
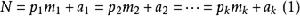 初等數論
初等數論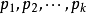 初等數論
初等數論其中
順序地表示素數2,3,5,...。對以上的諸
(
,即
為N被
相除所得之餘數 ),有
(餘數不為0)。即N不能是2m,3m,5m,...,pm形。若
,則N是一個素數。
(五)可以把上述的式(1)用同餘式組表示:
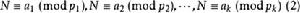 初等數論
初等數論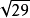 初等數論
初等數論例如,29不能夠被
以下的任何素數2,3,5整除,29=2x14+1=3x9+2=5x5+4。
29≡1(mod2),29≡2(mod3), 29≡4(mod5)。29小於7=49 ,所以29是一個素數。
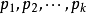 初等數論
初等數論由於(2)的模
兩兩互素,根據孫子定理(中國剩餘定理)知,(2)式在
的意義上有唯一解。
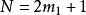 初等數論
初等數論例如k=1時,
,解得N=3,5,7。求得了(3,3)區間的全部素數。
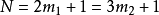 初等數論
初等數論k=2時,
,解得N=7,13,19;
,解得N=5,11,17,23。如此,求得了(5,5 )區間的全部素數。
仿此下去可以求得任意給定數以內的全部素數。
(六)用程式方法求素數。“若一個自然數n,判斷n/k是否整除,先判斷其能否整除2,若不能再判斷其能否整除3,依次向下判斷,當k>(n/k)時,判斷結束。”如果所有判斷都不能整除,則自然數N為素數。
公元3世紀,丟番圖研究了若干不定方程,並分別設計巧妙解法,故後人稱不定方程為丟番圖方程。17世紀以來,費馬、歐拉、高斯等人的工作大大豐富和發展了初等數論的內容。
古代中國
中國古代對初等數論的研究有著光輝的成就,《周髀算經》、《孫子算經》、《張邱建算經》、《數書九章》等古文獻上都有記載。孫子定理比歐洲早500年, 西方常稱此定理為中國剩餘定理,秦九韶的大衍求一術也馳名世界。初等數論不僅是研究純數學的基礎,也是許多學科的重要工具。它的套用是多方面的,如計算機科學、組合數學、密碼學、資訊理論等。如公開密鑰體制的提出是數論在密碼學中的重要套用。
初等數論內容
初等數論有以下幾部分內容:
1.整除理論。引入整除、因數、倍數、質數與合數等基本概念。這一理論的主要成果有:唯一分解定理、裴蜀定理、歐幾里德的輾轉相除法、算術基本定理、素數個數無限證明。
2.同餘理論。主要出自於高斯的《算術研究》內容。定義了同餘、原根、指數、平方剩餘、同餘方程等概念。主要成果:二次互反律、歐拉定理、費馬小定理、威爾遜定理、孫子定理(即中國剩餘定理)等等。
3.連分數理論。引入了連分數概念和算法等等。特別是研究了整數平方根的連分數展開。主要成果:循環連分數展開、最佳逼近問題、佩爾方程求解。
4.不定方程。主要研究了低次代數曲線對應的不定方程,比如勾股方程的商高定理、佩爾方程的連分數求解。也包括了四次費馬方程的求解問題等等。
5.數論函式。比如歐拉函式、莫比烏斯變換等等。
6.高斯函式。
初等數論是一個理論層次
第一個層次叫做數學概念,是反映對象的本質屬性的思維形式。人類在認識過程中,從感性認識上升到理性認識,把所感知的事物的共同本質特點抽象出來,加以概括,就成為概念。表達概念的語言形式是詞或詞組。科學概念,特別是數學概念要求更加嚴格,至少必須具備三個條件:專一性,精確性,可以檢驗。例如:”孿生素數“就是一個數學概念。
第二個層次叫做數學命題,數學命題是對一系列數學概念之間的關係作出判斷的句子。一個命題要么真,要么不真(這由邏輯中的排中律保證)。真命題包含定理,引理,推論,事實等。命題既可以是存在性命題(表述為”存在......."),也可以是全稱命題(表述為“對於一切.....")。
第三個層次叫做數學理論,把方法,公式,公理,定理,原理,組合成為一個體系叫做數學理論。例如“初等數論”,由公理(例如等量公理),定理(例如費馬小定理),原理(例如抽屜原理,一一對應原理),公式等組成。
在數學證明時,全稱命題常常不能通過枚舉法來判斷真偽,這是因為數學有時面對的是無窮多個對象,永遠不可能一一枚舉出每一種情況。不完全歸納法在數學中是不可行的,數學只承認演繹邏輯(數學歸納法,超限歸納法等均屬於演繹邏輯)。
代表人物
費馬
費馬在古典數論領域中的成果很多,比如提出了不定方程無解證明的無窮遞降法,引入了費馬數等等。
 費馬
費馬與費馬相關的著名結論如下:
費馬小定理:a^p-a≡0(mod p),其中p是一個素數,a是正整數。
事實上它是歐拉定理的一個特殊情況,Euler定理是說:a^φ(n)-1≡0(mod n),a,n都是正整數且互素,φ(n)是Euler函式,表示和n互素的小於n的正整數的個數。
費馬大定理(當時是猜想):n>2是整數,則方程x^n+y^n=z^n沒有滿足xyz≠0的整數解。這個是不定方程,它已經由美國數學家安德魯·懷爾斯證明了(1995年),證明的過程相當艱深。
歐拉
 歐拉
歐拉引入歐拉函式,得到著名的歐拉定理——費馬小定理推廣;研究了連分數展開問題;用解析方法證明了素數無限;討論平方和問題及哥德巴赫猜想——加性數論內容。
高斯
 高斯
高斯被譽為“數學王子”。解決了正多邊形尺規作圖問題,將它和費馬數聯繫起來。高斯的著作
《算術研究》提出了同餘理論,討論了平方剩餘問題,發現了二次互反律。高斯提出了著名的素數定理(當時是猜想),研究了指標和估計問題——表示論的雛形。
同名書籍
高等學校數學教材初等數論(第二版)定價:¥35.00
作者:潘承洞,潘承彪著
出 版 社:北京大學出版社
出版時間:2003-1-1
版次:2
頁數:592
字數:520000
印刷時間:2011-1-1
開本:大32開
紙張:膠版紙
印次:9
I S B N:9787301060759
包裝:平裝
內容簡介
本書自1992年9月出版以來,已發行24000冊,深受教師和學生的歡迎。在第二版中,本書作者根據10年來讀者和本書編輯提出的寶貴意見,以及在教學實踐中的體會,對本書內容做了進一步修改與完善(見第二版說明),使之更適宜於教學需要。
本書是大學初等數論課教材。全書共分九章。內容包括:整除,不定方程,同餘,同餘方程,指數與原根,連分數,素數分布的初等結果,數論函式等。書中配有較多的習題,書末附有提示與解答。?書積累了作者數十年教學與科研的經驗,遵循少而精的原則,精心選材。為便於學生理想,對重點內容多側面分析,從不同角度進行闡述。
作者簡介潘承洞,數學家,中科院院士。江蘇蘇州人。著作有《哥德巴赫猜想》(合著)、《階的估計》等。
目錄第二版說明
第一版序
符號說明
第一章整除
1自然數與整數
2整除
3帶餘數除法與輾轉相除法
4最大公約數理論
5算術基本定理(A)
6算術基本定理(B)
7符號[X],n!的分解式
8容斥原理與3.14……(X)的計算公式
第二章不定方程(I)
1一次不定方程
3X2+Y2=Z2
第三章同餘
1同餘
2同餘類與剩餘系
3(M)的性質與Fermat-Euler定理
4Wlison定理
第四章同餘方程
1同餘方程的基本概念
2一次同餘方程
3一次同餘方程組,孫子定理
4一般同餘方程的求解
5橫為素數的二次同餘方程
6Legendre符號,Gauss二次互反律
7Jacbi符號
8模為素數的高次同餘方程
9多元同餘方程,Chevalley定理
第五章指數與原根
1指數
2原根
3指標、指?組與既約剩餘系的構造
4二項同餘方程
第六章不定方程(II)
……
第七章連分數
第八章素數分布的初等結果
第九章數論函式
附錄一自然數
附錄二算術基本定理不成立的例子
附錄三初等數論的幾個套用
附錄四國際數學奧林匹克競賽中數論有關的題
習題的提示與解答

