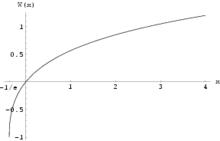
命名
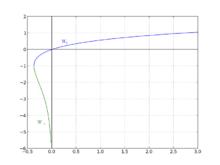 朗伯W函式兩個分支的圖像
朗伯W函式兩個分支的圖像 朗伯W函式
朗伯W函式朗伯W函式(Lambert W Function)由約翰·海因里希·朗伯(Johann HeinrichLambert)命名。在Digital Library of Mathematical Functions(儲存特殊函式的數學運用的一個網路項目)中主分支
 朗伯W函式
朗伯W函式被表示為
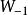 朗伯W函式
朗伯W函式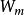 朗伯W函式
朗伯W函式,分支 被表示為 。
微分與積分
微分
 朗伯W函式
朗伯W函式滿足微分方程
 朗伯W函式
朗伯W函式所以
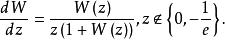 朗伯W函式
朗伯W函式此外,我們有
 朗伯W函式
朗伯W函式積分
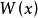 朗伯W函式
朗伯W函式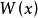 朗伯W函式
朗伯W函式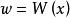 朗伯W函式
朗伯W函式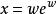 朗伯W函式
朗伯W函式函式 或一些包含 的表達式可運用代換 進行積分。( )
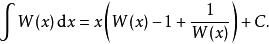 朗伯W函式
朗伯W函式特殊的有
 朗伯W函式
朗伯W函式漸近展開式
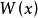 朗伯W函式
朗伯W函式函式 有泰勒展開式
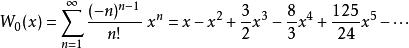 朗伯W函式
朗伯W函式 朗伯W函式
朗伯W函式收斂半徑為 。
 朗伯W函式
朗伯W函式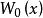 朗伯W函式
朗伯W函式對於大的數 , 有漸近展開式
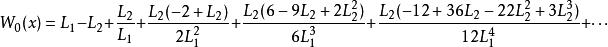 朗伯W函式
朗伯W函式和
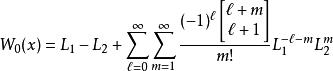 朗伯W函式
朗伯W函式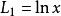 朗伯W函式
朗伯W函式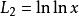 朗伯W函式
朗伯W函式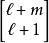 朗伯W函式
朗伯W函式其中 , , 是非負的第一類斯特靈數(Stirling number of the first kind)。
在展開式中只留前兩項
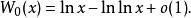 朗伯W函式
朗伯W函式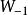 朗伯W函式
朗伯W函式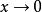 朗伯W函式
朗伯W函式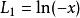 朗伯W函式
朗伯W函式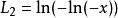 朗伯W函式
朗伯W函式另一分支 ,當 時有相似的漸進展開式, , 。
複數次方
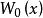 朗伯W函式
朗伯W函式的平方有泰勒公式
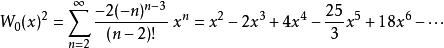 朗伯W函式
朗伯W函式 朗伯W函式
朗伯W函式更一般的情況下,當 是整數,有
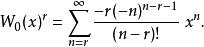 朗伯W函式
朗伯W函式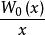 朗伯W函式
朗伯W函式 朗伯W函式
朗伯W函式的 次方有泰勒公式
 朗伯W函式
朗伯W函式 朗伯W函式
朗伯W函式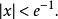 朗伯W函式
朗伯W函式其中 是任意複數,
恆等式
用朗伯W函式的定義,我們有
 朗伯W函式
朗伯W函式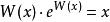 朗伯W函式
朗伯W函式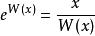 朗伯W函式
朗伯W函式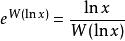 朗伯W函式
朗伯W函式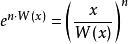 朗伯W函式
朗伯W函式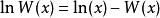 朗伯W函式
朗伯W函式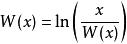 朗伯W函式
朗伯W函式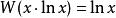 朗伯W函式
朗伯W函式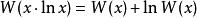 朗伯W函式
朗伯W函式特殊值
 朗伯W函式
朗伯W函式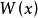 朗伯W函式
朗伯W函式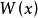 朗伯W函式
朗伯W函式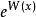 朗伯W函式
朗伯W函式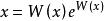 朗伯W函式
朗伯W函式當 為一非0的代數數時, 為超越數。如果 為非0的代數數,運用林德曼-魏爾斯特拉斯定理(Lindemann–Weierstrass theorem) , 一定是超越的,因此 也是超越數。
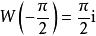 朗伯W函式
朗伯W函式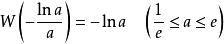 朗伯W函式
朗伯W函式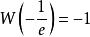 朗伯W函式
朗伯W函式 朗伯W函式
朗伯W函式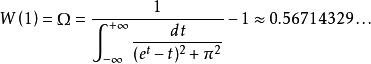 朗伯W函式
朗伯W函式 朗伯W函式
朗伯W函式其中 為歐米加常數(Omega constant) 。
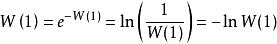 朗伯W函式
朗伯W函式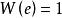 朗伯W函式
朗伯W函式 朗伯W函式
朗伯W函式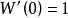 朗伯W函式
朗伯W函式舉例介紹
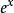 朗伯W函式
朗伯W函式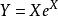 朗伯W函式
朗伯W函式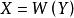 朗伯W函式
朗伯W函式朗伯W函式可以解許多包含指數函式 的方程。其中主要的方法是把所有未知數移向一邊,令方程變成 形式,解出 。
例子1
 朗伯W函式
朗伯W函式更一般的
 朗伯W函式
朗伯W函式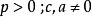 朗伯W函式
朗伯W函式其中 ,可以使用代換
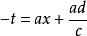 朗伯W函式
朗伯W函式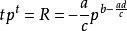 朗伯W函式
朗伯W函式解出
 朗伯W函式
朗伯W函式因此最後答案為
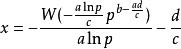 朗伯W函式
朗伯W函式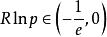 朗伯W函式
朗伯W函式如果 ,方程有第二個解
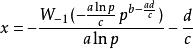 朗伯W函式
朗伯W函式例子2
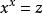 朗伯W函式
朗伯W函式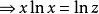 朗伯W函式
朗伯W函式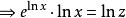 朗伯W函式
朗伯W函式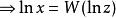 朗伯W函式
朗伯W函式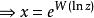 朗伯W函式
朗伯W函式或
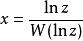 朗伯W函式
朗伯W函式因為根據定義,有
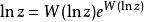 朗伯W函式
朗伯W函式例子3
 朗伯W函式
朗伯W函式關於超-4運算(tetration,另見超運算)的方程
 朗伯W函式
朗伯W函式如果超運算收斂至一個數 ,則
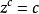 朗伯W函式
朗伯W函式解出
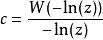 朗伯W函式
朗伯W函式例子4
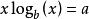 朗伯W函式
朗伯W函式的解為
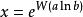 朗伯W函式
朗伯W函式例子5
延遲微分方程(delay differential equation)
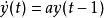 朗伯W函式
朗伯W函式 朗伯W函式
朗伯W函式的特徵方程為
解出
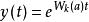 朗伯W函式
朗伯W函式 朗伯W函式
朗伯W函式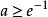 朗伯W函式
朗伯W函式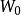 朗伯W函式
朗伯W函式其中 為朗伯W函式的分支。如果 ,則只用考慮其主分支 。
數值估算
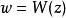 朗伯W函式
朗伯W函式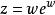 朗伯W函式
朗伯W函式朗伯W函式可以用牛頓疊代法(Newton's method)求其近似值 使 。
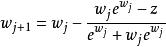 朗伯W函式
朗伯W函式函式亦可以使用哈雷疊代法(Halley's method)求近似值。
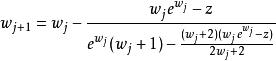 朗伯W函式
朗伯W函式