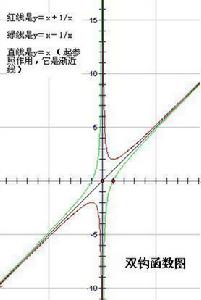
該函式是奇函式,圖象關於原點對稱。位於第一、三象限。
若且唯若ax=b/x,即x=√(b/a)時取等號。
故其頂點坐標為(√(b/a),2√ab),圖象在(0,√(b/a))上是單調遞減的,在(√(b/a),+∝)上是單調遞增
同理:當x<0時,由基本不等式可得:y≤-2√ab
若且唯若ax=b/x,即x=-√(b/a)時取等號。
故其頂點坐標為(-√(b/a),-2√ab),
圖象在(-∝,-√(b/a))上是單調遞增,
在(-√(b/a),0)上是單調遞減的.
當a<0,b<0 時可轉化為a>0,b>0的情況
下面我們證明函式f(x)=ax+b/x,(a>0,b>0)在x>0上的單調性
設x1>x2且x1,x2∈(0,+∝)
則f(x1)-f(x2)=(ax1+b/x1) -(ax2+b/x2)
=a(x1-x2)-b(x1-x2)/x1x2
=(x1-x2)(ax1x2-b)/x1x2
因為x1>x2,則x1-x2>0
當x∈(0,√(b/a))時,x1x2<b/a
則ax1x2-b<b-b=0
所以f(x1)-f(x2)<0,即x∈(0,√(b/a))時,f(x)=ax+b/x單調遞減;
當x∈(√(b/a),+∞)時,x1x2>b/a
則ax1x2-b>b-b=0
所以f(x1)-f(x2)>0,即x∈(√(b/a),+∞)時,f(x)=ax+b/x單調遞增。
