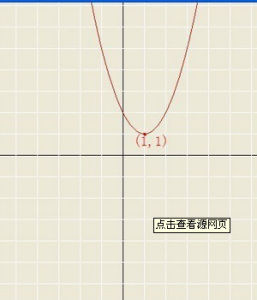
二次函式拋物線頂點式&頂點坐標
頂點式:y=a(x-h)^2+k (a≠0,k為常數,x≠h)
頂點坐標:(-b/2a,(4ac-b^2)/4a)
解釋
在二次函式的圖像上
頂點式:y=a(x-h)^2;+k 拋物線的頂點P(h,k)
頂點坐標:對於二次函式 y=ax^2;+bx+c 其頂點坐標為 (-b/2a,(4ac-b^2;)/4a)
考點掃描
1.會用描點法畫出二次函式的圖象.
 頂點坐標
頂點坐標2.能利用圖象或配方法確定拋物線的開口方向及對稱軸、頂點的位置.
3.會根據已知圖象上三個點的坐標求出二次函式的解析式.
名師講解
1.二次函式y=ax²,y=a(x-h)²,y=a(x-h)²+k,y=ax²+bx+c(各式中,a≠0)的圖象形狀相同,只是位置不同,它們的頂點坐標及對稱軸如下表:
解析式
y=ax²
y=a(x-h)²
y=a(x-h)²+k
y=ax²+bx+c
頂點坐標
[0,0]
[h,0]
[h,k]
[-b/2a,(4ac-b²)/4a]
對稱軸
x=0
x=h
x=h
x=-b/2a
當h>0時,y=a(x-h)²的圖象可由拋物線y=ax²向右平行移動h個單位得到,
當h<0時,則向左平行移動|h|個單位得到.
當h>0,k>0時,將拋物線y=ax²向右平行移動h個單位,再向上移動k個單位,就可以得
 頂點坐標
頂點坐標當h>0,k<0時,將拋物線y=ax²向右平行移動h個單位,再向下移動|k|個單位可得到y=a(x-h)²+k的圖象;
當h<0,k>0時,將拋物線向左平行移動|h|個單位,再向上移動k個單位可得到y=a(x-h)²+k的圖象;
當h<0,k<0時,將拋物線向左平行移動|h|個單位,再向下移動|k|個單位可得到y=a(x-h)²+k的圖象;
因此,研究拋物線y=ax2+bx+c(a≠0)的圖象,通過配方,將一般式化為y=a(x-h)²+k的形式,可確定其頂點坐標、對稱軸,拋物線的大體位置就很清楚了.這給畫圖象提供了方便.
2.拋物線y=ax²+bx+c(a≠0)的圖象:當a>0時,開口向上"當a<0時,開口向下,對稱軸是直線x=-b/2a,頂點坐標是[ -b/2a,(4ac-b²)/4a]
3.拋物線y=ax²+bx+c(a≠0),若a>0,當x≤-b/2a時,y隨x的增大而減小;當x≥-b/2a時,y隨x的增大而增大.若a<0,當x≤-b/2a時,y隨x的增大而增大;當x≥-b/2a時,y隨x的增大而減小.4.拋物線y=ax²+bx+c的圖象與坐標軸的交點:
(1)圖象與y軸一定相交,交點坐標為(0,c);
(2)當△=b2-4ac>0,圖象與x軸交於兩點A(x1,0)和B(x2,0),其中的x1,x2是一元二次方程ax²+bx+c=0
(a≠0)的兩根.這兩點間的距離AB=|x2-x1|=.
當△=0.圖象與x軸只有一個交點;
當△<0.圖象與x軸沒有交點.當a>0時,圖象落在x軸的上方,x為任何實數時,都有y>0;當a<0時,圖象落在x軸的下方,x為任何實數時,都有y<0.
5.拋物線y=ax²+bx+c的最值:如果a>0(a<0),則當x=時,y最小(大)值=.
頂點的橫坐標,是取得最值時的自變數值,頂點的縱坐標,是最值的取值.
6.用待定係數法求二次函式的解析式
(1)當題給條件為已知圖象經過三個已知點或已知x、y的三對對應值時,可設解析式為一般形式:
y=ax²+bx+c(a≠0).
(2)當題給條件為已知圖象的頂點坐標或對稱軸時,可設解析式為頂點式:y=a(x-h)²+k(a≠0).
(3)當題給條件為已知圖象與x軸的兩個交點坐標時,可設解析式為兩根式:y=a(x-x1)(x-x2)(a≠0).
7.二次函式知識很容易與其它知識綜合套用,而形成較為複雜的綜合題目。因此,以二次函式知識為主的綜合性題目是中考的熱點考題,往往以大題形式出現.
二次函式常用的一般形式
1.y=ax^2+bx+c(a≠0)
2.y=ax^2(a≠0)
3.y=ax^2+c(a≠0)
4.y=a(x-h)^2(a≠0)
5.y=a(x-h)^2+k(a≠0)←頂點式
6.y=a(x-x1)(x-x2)(a≠0)←交點式