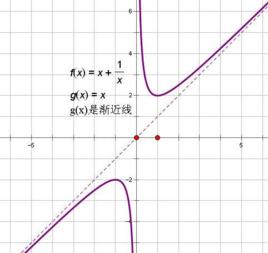
函式定義
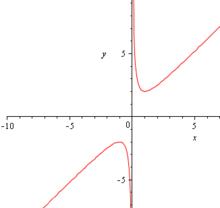 對勾函式
對勾函式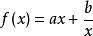 對勾函式
對勾函式所謂的對勾函式(雙曲函式),是形如(a>0,b>0)的函式。
性質
圖像
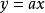 對勾函式
對勾函式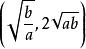 對勾函式
對勾函式對勾函式是數學中一種常見而又特殊的函式,見圖示,在作圖時最好畫出漸近線。在第一象限內,其轉折點為
最值
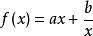 對勾函式
對勾函式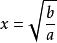 對勾函式
對勾函式當x>0時,有最小值(這裡為了研究方便,規定a>0,b>0),也就是當時,f(x)取最小值。
奇偶、單調性
奇偶性
雙勾函式是奇函式。
單調性
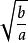 對勾函式
對勾函式令k=,那么:
增區間:{x|x≤-k}和{x|x≥k};減區間:{x|-k≤x<0}和{x|0<x≤k}
變化趨勢:在y軸左邊先增後減,在y軸右邊先減後增,是兩個勾。
漸近線
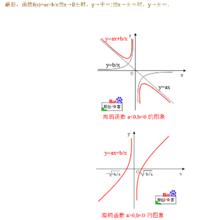 對勾函式
對勾函式對勾函式的圖像是分別以y軸和y=ax為 漸近線的兩支曲線,且圖像上任意一點到兩條漸近線的 距離之積恰為漸近線夾角(0-180°)的 正弦值與|b|的乘積。
註:對勾函式的圖像是雙曲線。實際上該圖像是軸對稱的,並可以通過雙曲線的標準方程通過旋轉角度得到。
均值不等式
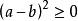 對勾函式
對勾函式對勾函式性質的研究離不開均值不等式。說到均值不等式,其實也是根據二次函式得來的。我們都知道
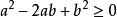 對勾函式
對勾函式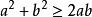 對勾函式
對勾函式展開,得 ,即 .
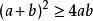 對勾函式
對勾函式兩邊同時加上2ab,整理得 ,
兩邊開平方,就得到了均值定理的公式:
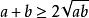 對勾函式
對勾函式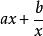 對勾函式
對勾函式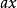 對勾函式
對勾函式 對勾函式
對勾函式將 中 看做a, 看做b代入上式,得
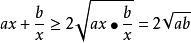 對勾函式
對勾函式這裡有個規定:若且唯若ax=b/x時取到最小值,解出x=sqrt(b/a),對應的f(x)=2sqrt(ab)。我們再來看看均值不等式,它也可以寫成這樣:(a+b)/2≥sqrt(ab),前式大家都知道,是求平均數的公式。那么後面的式子呢?也是平均數的公式,但不同的是,前面的稱為算術平均數,而後面的則稱為幾何平均數,總結一下就是算術平均數絕對不會小於幾何平均數。
導數求解
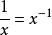 對勾函式
對勾函式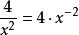 對勾函式
對勾函式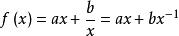 對勾函式
對勾函式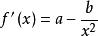 對勾函式
對勾函式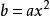 對勾函式
對勾函式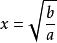 對勾函式
對勾函式其實用導數也可以研究 對勾函式的性質。不過首先要會負指數冪的換算,這也很簡單,但要熟練掌握。舉幾個例子:,。x為分母的時候可以轉化成負指數冪。那么就有,求導方法一樣,求得的導函式為,令f'(x)=0,計算得到,結果仍然是,如果需要的話算出f(x)就行了。平時做題的時候用導數還是均值定理,就看你喜歡用哪個了。不過注意均值定理最後的討論,有時ax≠b/x,就不能用均值定理了。
上述研究都是建立在x>0的基礎上的,不過對勾函式是奇函式,所以研究出正半軸圖像的性質後,自然能補出對稱的圖像。如果出現平移了的問題(圖像不再規則),就先用平移公式或我總結出的平移規律還原以後再研究,這個能力非常重要,一定要多練,爭取做到特別熟練的地步。
事實上,利用將對勾函式進行選擇可以得到標準的雙曲線方程。也就是說,對勾函式是雙曲線,這個利用二階矩陣的變換也是可以得到的。
另外對於二次曲線,它只可能是以下幾種情況:圓,橢圓,雙曲線,拋物線,或者是兩條直線。
由對勾函式的圖像看出來,非雙曲線莫屬了。
其它解法
面對這個函式 f(x)=ax+b/x ,我們應該想得更多,需要我們深入探究:⑴它的單調性與奇偶性有何套用?而值域問題恰好與單調性密切相關,所以命題者首先想到的問題應該與值域有關;⑵函式與方程之間有密切的聯繫,所以命題者自然也會想到函式與方程思想的運用;⑶眾所周知,雙曲線中存在很多定值問題,所以很容易就想到定值的存在性問題。因此就由特殊引出了一般結論;繼續拓展下去,用所猜想、探索的結果來解決較為複雜的函式最值問題。能否與均值有關係。
重點
對勾函式的一般形式是:
f(x)=ax+b/x(a>0) 不過在高中文科數學中a多半僅為1,b值不定。理科數學變化更為複雜。
定義域為(-∞,0)∪(0,+∞)
值域為(-∞,-2√ab]∪[2√ab,+∞)
當x>0,有x=根號b/根號a,有最小值是2√ab
當x<0,有x=-根號b/根號a,有最大值是:-2√ab
對勾函式的解析式為y=x+a/x(其中a>0),它的單調性討論如下:
設x1<x2,則f(x1)-f(x2)=x1+a/x1-(x2+a/x2)=(x1-x2)+a(x2-x1)/(x1x2)=[(x1-x2)(x1x2-a)]/(x1x2)
下面分類進行討論:
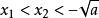 對勾函式
對勾函式⑴ 當 時 ,x1-x2<0,x1x2-a>0,x1x2>0,所以f(x1)-f(x2)<0,即f(x1)<f(x2),所以函式在(-∞,-根號a)上是增函式
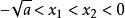 對勾函式
對勾函式⑵當 時,x1-x2<0,x1x2-a<0,x1x2>0,所以f(x1)-f(x2)>0,即f(x1)>f(x2),所以函式在(-根號a,0)上是減函式
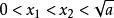 對勾函式
對勾函式⑶當 時 ,x1-x2<0,x1x2-a<0,x1x2>0,所以f(x1)-f(x2)>0,即f(x1)>f(x2),所以函式在(0,根號a)上是減函式
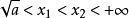 對勾函式
對勾函式⑷當 時 ,x1-x2<0,x1x2-a>0,x1x2>0,所以f(x1)-f(x2)<0,即f(x1)<f(x2),所以函式在(根號a,+∞)上是增函式
解題時常利用此函式的單調性求最大值(max)與最小值(min)。
例題
2006年高考上海數學試卷(理工農醫類)
已知函式 y=x+a/x 有如下性質:如果常數a>0,那么該函式在 (0,√a] 上是減函式,在 ,[√a,+∞)上是增函式.
⑴如果函式 y=x+(2^b)/x (x>0)的值域為 [6,+∞),求b 的值;
⑵研究函式 y=x^2+c/x^2 (常數c >0)在定義域內的單調性,並說明理由;
⑶對函式y =x+a/x 和y =x^2+a/x^2(常數a >0)作出推廣,使它們都是你所推廣的函式的特例.研究推廣後的函式的單調性(只須寫出結論,不必證明),並求函式F(x) =(x^2+1/x)^n+(1/x^2+x)^n(n是正整數)在區間[1/2;,2]上的最大值和最小值(可利用你的研究結論)