幾何與方程論
Functions images(函式的圖象)
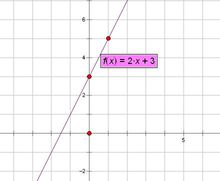一次函式圖像點集{(x，y)丨y=x}
叫做函式y=x的圖象
一次函式
自變數x和因變數y有如下關係：
y=kx+b（k，b為常數，k≠0）
則稱y是x的一次函式。
特別地，當b=0時，y是x的正比例函式。
若兩個變數x，y間的關係式可以表示為y=kx+b（k，b為常數，k≠0）的形式，則稱y是x的一次函式（x為自變數，y為因變數）。特別地，當b=0時，稱y是x的正比例函式。
圖象性質
1． 作法與圖形：通過如下3個步驟（1）算出該函式圖象與Y軸和X軸的交點的坐標（2）描點；（3）連線，可以作出一次函式的圖象——一條直線。
2． 性質：在一次函式上的任意一點P（x，y），都滿足等式：y=kx+b。
3． k，b與函式圖象所在象限。
當k>0時，直線必通過一、三象限，從左往右，y隨x的增大而增大；
當k<0時，直線必通過二、四象限，從左往右，y隨x的增大而減小；
當b>0時，直線必通過一、二象限；當b<0時，直線必通過三、四象限。
特別地，當b=O時，直線通過原點O（0，0）表示的是正比例函式的圖象。
這時，當k>0時，直線只通過一、三象限；當k<0時，直線只通過二、四 象限。
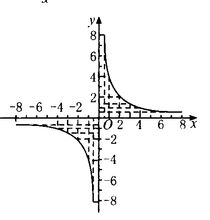反比例函式圖像4. （1) 函式關係中自變數可取值的集合叫做函式的定義域。
求用解析式表示的函式的定義域，就是求使函式各個組成部分有意義的集合的交集，對實際問題中函式關係定義域，還需要考慮實際問題的條件。 (2)值域與定義域內的所有x值對應的函式值形成的集合，叫做函式的值域。（3)單調性定義：對於給定區間上的函式f(x)。
例題
已知點A（x1，y1）；B（x2，y2），請確定過點A、B的一次函式的表達式。 （1）設一次函式的表達式（也叫解析式）為y=kx+b。如果b=0，則函式解析式為y=kx,所以說正比例函式是特殊的一次函式。 （2）因為在一次函式上的任意一點P（x，y），都滿足等式y=kx+b。所以可以列出2個方程： y1=kx1+b① 和y2=kx2+b②。 （3）解這個二元一次方程，得到k，b的值。 （4）最後得到一次函式的表達式。 （5）在y=kx+b中,使x,y分別等於0，可求出兩個坐標系必定經過的兩點(0,b)和(-b/k,0)。
套用
1.當時間t一定，距離s是速度v的一次函式。s=vt。
2.當水池抽水速度f一定，水池中水量g是抽水時間t的一次函式。設水池中原有水量S。g=S-ft。
分類
反比例函式
形如 y=k/x(k為常數且k≠0) 的函式，叫做反比例函式。
自變數x的取值範圍是不等於0的一切實數。
反比例函式的圖象為雙曲線。
如圖，上面給出了x分別為正和負（2和-2), k=4 時的函式圖象。
雙鉤函式
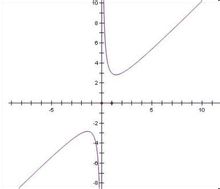雙鉤函式圖像函式f(x)=ax+b/x,(a>0,b>0)叫做雙鉤函式。
該函式是奇函式，圖象關於原點對稱。位於第一、三象限。
當x>0時，由基本不等式可得：y ≥2√ab
若且唯若ax=b/x,即x=√(b/a)時取等號。
故其頂點坐標為(√(b/a)，2√ab)，圖象在(0，√(b/a))上是單調遞減的，在(√(b/a)，+∝)上是單調遞增
同理：當x<0時，由基本不等式可得：y≤-2√ab
若且唯若ax=b/x,即x=-√(b/a)時取等號。
故其頂點坐標為(-√(b/a)，-2√ab)，
圖象在(-∝，-√(b/a))上是單調遞增，
在(-√(b/a)，0)上是單調遞減的。
當a<0,b<0 時可轉化為a>0,b>0的情況
通常，作圖時，x看做0。代入得y，也就是縱軸坐標(0，y)
有時，通過平移，把形如y=(ax+b)/(cx+d)也看成反比例函式。
特殊位置關係
當平面直角坐標系中兩直線平行時，其函式解析式中K值（即一次項係數）相等
當平面直角坐標系中兩直線垂直時，其函式解析式中K值互為負倒數（即兩個K值的乘積為-1）
二次函式
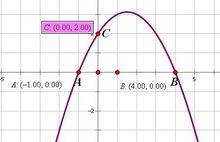二次函式圖像一般地，自變數x和因變數y之間存在如下關係：
（a，b，c為常數，a≠0，且a決定函式的開口方向，a>0時，開口方向向上，a<0時，開口方向向下,IaI還可以決定開口大小,IaI越大開口就越小,IaI越小開口就越大.）
則稱y為x的二次函式。
二次函式表達式的右邊通常為二次三項式。
表達式
一般式：y=ax^2+bx+c（a，b，c為常數，a≠0）
頂點式：y=a(x-h)^2+k [拋物線的頂點P（h，k）]
交點式：y=a(x-x₁)(x-x ₂) [僅限於與x軸有交點A（x₁ ，0）和 B（x₂，0）的拋物線]
註：在3種形式的互相轉化中，有如下關係:
h=-b/2a k=(4ac-b^2)/4a x₁,x₂=(-b±√b^2-4ac)/2a
圖象
在平面直角坐標系中作出二次函式y=x^2的圖象，
可以看出，二次函式的圖象是一條拋物線。
性質
1.拋物線是軸對稱圖形。對稱軸為直線x = -b/2a。
對稱軸與拋物線唯一的交點為拋物線的頂點P。
特別地，當b=0時，拋物線的對稱軸是y軸（即直線x=0）
2.拋物線有一個頂點P，坐標為P ( -b/2a ，(4ac-b^2)/4a )
當-b/2a=0時，P在y軸上；當Δ= b^2-4ac=0時，P在x軸上。
3.二次項係數a決定拋物線的開口方向和大小。
當a>0時，拋物線向上開口；當a<0時，拋物線向下開口。
|a|越大，則拋物線的開口越小。
4.一次項係數b和二次項係數a共同決定對稱軸的位置。
當a與b同號時（即ab>0），對稱軸在y軸左；
當a與b異號時（即ab<0），對稱軸在y軸右。
5.常數項c決定拋物線與y軸交點。
拋物線與y軸交於（0，c）
6.拋物線與x軸交點個數
Δ= b方-4ac>0時，拋物線與x軸有2個交點。
Δ= b方-4ac=0時，拋物線與x軸有1個交點。
Δ= b方-4ac<0時，拋物線與x軸沒有交點。X的取值是虛數（x= -b±√b^2－4ac 的值的相反數，乘上虛數i，整個式子除以2a）
位置關係
二次函式y=ax^2，y=a(x-h)^2，y=a(x-h)^2 +k，y=ax^2+bx+c(各式中，a≠0)的圖象形狀相同，只是位置不同，它們的頂點坐標及對稱軸如下表：
解析式 頂點坐標 對 稱 軸
y=ax^2 (0，0) x=0
y=a(x-h)^2 (h，0) x=h
y=a(x-h)^2+k (h，k) x=h
y=ax^2+bx+c (-b/2a，[4ac-b^2]/4a) x=-b/2a
當h>0時，y=a(x-h)^2的圖象可由拋物線y=ax^2向右平行移動h個單位得到，
當h<0時，則向左平行移動|h|個單位得到．
當h>0,k>0時，將拋物線y=ax^2向右平行移動h個單位，再向上移動k個單位，就可以得到y=a(x-h)^2 +k的圖象；
當h>0,k<0時，將拋物線y=ax^2向右平行移動h個單位，再向下移動|k|個單位可得到y=a(x-h)^2+k的圖象；
當h<0,k>0時，將拋物線向左平行移動|h|個單位，再向上移動k個單位可得到y=a(x-h)^2+k的圖象；
當h<0,k<0時，將拋物線向左平行移動|h|個單位，再向下移動|k|個單位可得到y=a(x-h)^2+k的圖象；
因此，研究拋物線 y=ax^2+bx+c(a≠0)的圖象，通過配方，將一般式化為y=a(x-h)^2+k的形式，可確定其頂點坐標、對稱軸，拋物線的大體位置就很清楚了．這給畫圖象提供了方便．
2．拋物線y=ax^2+bx+c(a≠0)的圖象：當a>0時，開口向上，當a<0時開口向下，對稱軸是直線x=-b/2a，頂點坐標是(-b/2a，[4ac-b^2]/4a)．
3．拋物線y=ax^2+bx+c(a≠0)，若a>0，當x ≤ -b/2a時，y隨x的增大而減小；當x ≥ -b/2a時，y隨x的增大而增大．若a<0，當x ≤ -b/2a時，y隨x的增大而增大；當x ≥ -b/2a時，y隨x的增大而減小．
4．拋物線y=ax^2+bx+c的圖象與坐標軸的交點：
(1)圖象與y軸一定相交，交點坐標為(0，c)；
(2)當△=b^2-4ac>0，圖象與x軸交於兩點A(x₁，0)和B(x₂，0)，其中的x1,x2是一元二次方程ax^2+bx+c=0
(a≠0)的兩根．這兩點間的距離AB=|x₂-x₁|
當△=0．圖象與x軸只有一個交點；
當△<0．圖象與x軸沒有交點．當a>0時，圖象落在x軸的上方，x為任何實數時，都有y>0；當a<0時，圖象落在x軸的下方，x為任何實數時，都有y<0．
5．拋物線y=ax^2+bx+c的最值：如果a>0(a<0)，則當x= -b/2a時，y最小(大)值=(4ac-b^2)/4a．
頂點的橫坐標，是取得最值時的自變數值，頂點的縱坐標，是最值的取值．
