機率自動機論

機率自動機論，自動機論的次級學科，主要研究所處環境或內部具有（有限或無限的）隨機因素的自動機。

機率自動機論

與非機率型自動機不同之處，是機率自動機的動作是隨機的。為了給定機率自動機,首先必需規定在自動機處於某一狀態,並向自動機輸入某個字母的條件下，自動機下一動作（如狀態轉移，輸出某個字母，改寫字母等）的條件機率函式。其次是給定自動機的初始狀態的機率分布──初始分布，一般用一個隨機矢量π＝(π1，π2，…，πn)表示，其中各個πi都是非負的，且相加之和等於1。n是自動機狀態的個數。 πi表示在開始時自動機處於第i個狀態的機率。包含有不可靠元件的數字電路和通信的信道都可以表示為機率自動機。

機率自動機論

發展簡況　早在40年代末，C.E.仙農在資訊理論的研究中，就提出了噪聲信道的數學模型(見圖)，它實際上就是一種機率自動機。50年代初，J.諾伊曼研究用不可靠元件構造可靠機器，這個問題發展成為現代的容錯計算問題。但是直到50年代末，在R.W.阿西貝的著作中才給出一個形式定義的雛形。1963年M.O.拉賓比較嚴格地闡述了機率自動機的一些基本概念，並提出一些問題（如穩定性問題）。後來，A.帕茲等人的著作綜述了這一方面的研究成果。60年代末至70年代，有更多的人進行了這方面的研究工作。
主要內容　與一般的自動機理論相平行的，有機率圖靈機、機率時序機、機率識別器等方面的研究工作。這些工作一方面是推廣自動機已有的結果；另一方面也提出不少新的問題，豐富了自動機論的內容。
機率圖靈機　機率圖靈機是圖靈機的推廣。它的形式定義可以用六元組M=(X,Y,Q,W,p,π)給出。其中Q和W分別是非空有限的狀態集合和帶字母集合。X和Y 分別是輸入字母集合和輸出字母集合，且X∪Y吇W，Q∩W=Φ。π是初始分布。p(z,q′|q,ω)是已知機率圖靈機現在的狀態q,且注視在帶字母ω 的條件下它的“下一動作”的機率。“下一動作”是下面三者之一。①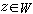:用z代替ω，且轉移到狀態q′；②z=R：讀寫頭向右移一單元,且轉移到狀態q′；③z＝L：讀寫頭向左移一單元，且轉移到狀態q′。
在機率圖靈機的研究中，對可計算隨機函式，給出了定義並對可計算函式及其運算也都作了研究，而且還證明了圖靈機的許多研究結果在機率圖靈機的情況下仍然成立。函式代入、原始遞歸、求極小等運算對可計算隨機函式都是封閉的。限制在普通函式類的範圍內，可以證明部分可計算隨機函式中的普通函式，恰好是部分遞歸函式。從這個意義上看，把圖靈機推廣到機率圖靈機的計算能力沒有增大。也可以通過別的刻劃方法，使機率圖靈機所刻劃的普通函式類，以部分遞歸函式類作為其真子類。在相對可計算性方面也有類似的結果。
機率時序機　它是時序機（見有限自動機論）的推廣。其形式定義可以用五元組M＝(X，Y，Q，p，π)給出，其中X，Y，Q，π仍如前所述，p是條件機率

p(y;q′|q;x)

x∈X　 y∈Y　q,q′∈Q

機率時序機被構想為理想化了的離散物理系統。它有有限個不同的內部狀態，而且有下面兩種性質：①如果現時狀態是q,輸入字母x,則p(y;q′|q;x)表示輸出的字母是y，並且下一時刻狀態為q′的聯合條件機率:②如果時序機開始時處於狀態 q1，並且輸入字母依次是x1，x2，…，xn，則輸出字母序列y1，y2，…，yn的機率是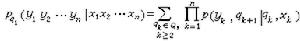

仙農首先用這一數學模型描述離散噪聲通信信道。因而關於機率時序機所得到的結果，既可以解釋為非機率時序機理論所得結果的對應推廣，又可以解釋為有限狀態通信信道的結構性質。
如果q1，q2∈Q，並且對於每一個正整數n

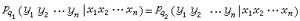
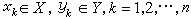對所有的都成立，就稱狀態q1和q2是等價的。等價狀態產生相同的“輸入－輸出關係”。研究狀態等價的充分必要條件，是機率時序機理論的研究內容之一。
如同在非機率時序機情況，多餘的等價狀態可以被消除，從而得到一個化簡了的時序機。對於機率時序機，它的化簡了的形式不是唯一的，這一點和確定的時序機的情況有所不同。對於一個給定的機率時序機，可以找到一個尋求它的所有化簡形式的計算方法。
機率有限識別器　只有輸入沒有輸出的有限識別器的推廣。它的形式定義可以用M＝(X，Q，p，π，F)給出。其中X和Q仍表示輸入字母表和狀態集合，π是初始分布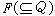，是規定的終止狀態集合。p(qj│qi，x)是當輸入一個字母x時,狀態從qi轉移到qj的機率,簡記為pij(x)。p(x)為以pij(x)為元素的矩陣。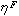是一個列矢量,它的維數等於Q內元素的個數,它相應於F中的元素的分量等於1,其餘的分量都是0,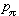(x1x2…xκ)=π·p(x1)·p(x2)p(xκ)·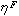表示以π為初始分布,輸入字x1x2…xκ後，狀態進入終止集合 F的機率。假定預先給定一個門限值λ(0≤λ＜1),則所有使得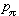(x1x2…xκ)＞λ的字x1x2…xκ構成一個集合,稱為機率有限識別器按切斷點λ所識別的（或接受的）的隨機語言,用集合的記號記為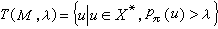

X*是X中的字母所能構成的一切字的集合。
隨機語言類包含有限識別器所識別的正則語言類作為其真子類，因而機率有限識別器是有限識別器的真推廣。隨機語言類對運算的封閉性，它的結構以及它與正則語言類的關係都是研究的重要內容。另一個問題是所謂穩定性問題。即對一個給定的機率識別器，轉移機率的微小擾動所引起的T(M,λ)中變化情況的研究。
多階段判決過程　機率自動機也可以用於多階段判決過程。在這一過程中，從一個狀態到另一狀態的轉移都附有一個條件機率和補償因子。假設對n個狀態的機率自動機從狀態qi轉移到狀態qj的補償因子是eij,則對於機率自動機在qi處一步轉移中的補償的數學期望值是

由此可以求出在κ步之後的全部補償。
機率自動機的熵　定義機率自動機的熵為

其中 pi(κ)是自動機在κ步轉移之後處於狀態qi的機率。熵的概念可以用於模式識別和可靠性問題的研究。用機率自動機描述不可靠自動機時，熵可以作為有限自動機的可靠性的測度。可靠性隨著熵的減小而增加，可靠自動機的熵是零。
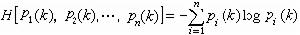
機率自動機理論與資訊理論、可靠性理論、自學習理論和模式識別、控制論、程式設計和馬爾可夫鏈的函式理論都有著密切的聯繫。圖靈機，各型形式語言的機率性推廣，具有機率性結構的樹自動機，機率自動機與動態規劃的關係，以及從範疇論觀點對隨機自動機的研究，都是一些有意義的研究課題。

配圖

相關連線