簡介
 隨機序列
隨機序列隨機數列的概念在機率論和統計學中都十分重要。整個概念主要構建在由隨機變數組成的數列的基礎之上,因此每每提及到隨機數列,人們常常會這樣開場:“設 為隨機變數……”但是也如同美國數學家得瑞克·亨利·雷莫在1951年時說的那樣:“隨機數列是一個很模糊的概念……它每一項都是無法預測中的無法預測,但是這些數字卻能夠通過傳統的統計學上的考驗。”
機率公理有意繞過了對隨機數列的定義。傳統的統計學理論並沒有直接闡明某個數列是否隨機,而是直接跳過這部分,在假設某種隨機性存在的前提之下討論隨機變數的性質。比如布爾巴基學派就認為,‘假設一個隨機數列’這句話是對術語的濫用。
歷史發展
法國數學家埃米爾·博雷爾是1909年第一批給出隨機性的正式定義的數學家之一。在1919年,受大數定理的啟發,奧地利數學家理察·馮·米澤斯給出了第一個算法隨機性的定義。但是,他使用了“集合”這個詞,而不是“隨機數列”。利用賭博系統的不可能性,馮·米澤斯定義道:若由0和1構成的無窮數列具有“頻率穩定性的特點”,也就是說,0的頻率趨進於1/2,且該數列的每個“以適當方式選取的”子數列也都沒有偏差,那么我們說,這個數列是“隨機的”。
馮·米澤斯的這個方法中,“適當選取子數列”的標準非常重要,因為雖然說“01010101……”本身沒有偏差(0齣現的機率為1/2),但是若我們只選奇數位置上的數字,得到的子數列便成了完全不隨機的“000000……”。馮·米澤斯未曾就這個問題正式給出一個選取規則上的解釋。1940年,美國數學家阿隆佐·邱奇將這個規則定義為“任何已經讀取該無窮數列的前N項,並決定是否讀取其第N+1項的遞歸函式。”邱其是可計算函式方面的先驅,他給出的這個定義的可計算性基於邱奇-圖靈猜想。這個定義經常被稱作“米澤斯-邱其隨機性”(英文:Mises-Church randomness)。
定義
隨機序列的產生為了形容隨機變數形成的序列。
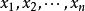 隨機序列
隨機序列 隨機序列
隨機序列 隨機序列
隨機序列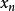 隨機序列
隨機序列一般的,如果用 (表示 下標於 )代表隨機變數,這些隨機變數如果按照順序出現,就形成了隨機序列,記做 (表示n上標於x)。這種隨機序列具備兩種關鍵的特點:其一,序列中的每個變數都是隨機的;其二,序列本身就是隨機的。
舉例說明
為了說明什麼是隨機序列,這裡來舉兩個例子。
 隨機序列
隨機序列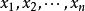 隨機序列
隨機序列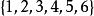 隨機序列
隨機序列假設持續扔一個骰子,會得到一系列隨機數,即1到6的整數,將連續擲骰子作為一個事件,那么這個事件應該包括扔第一次骰子得到的點數,扔第二次得到的點數,直到扔第 次得到的點數。把每次扔的的點數按順序分別記做 。這裡每個X的取值可能為 。那么我們可以寫出隨機序列:
 隨機序列
隨機序列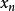 隨機序列
隨機序列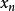 隨機序列
隨機序列 隨機序列
隨機序列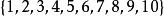 隨機序列
隨機序列 隨機序列
隨機序列更實際的,可以用高速路收費站來說明。假設一個收費站有10個出口。那么,把收費站出口出去的車數記做隨機變數 ,這裡 就是集合 ,集合中每個元素的取值為 。那么如果按照時間順序觀察,不難得出一個隨機序列,這個序列表示出口出去車數的一個變化情況,是一個序列,記做: 。
處理隨機數列的方式
現如今,有三個處理隨機序列的方式:
1.頻率-測量理論法
這個方法建立在前文的米澤斯和邱其的方法的基礎之上。 在1960年代,佩爾·馬丁-洛夫注意到,人們能夠寫下基於頻率生成隨機數列的代碼,而這些代碼的 集合是一種特殊的零測度集。在此基礎之上,通過利用所有的零測度集,人們能夠得到一個更加放之四海而皆準的隨機序列定義。
2.複雜度-可壓縮度法
 隨機序列
隨機序列 隨機序列
隨機序列 隨機序列
隨機序列 隨機序列
隨機序列柯爾莫哥洛夫本人對這個方法貢獻巨大,其次還有列文和阿根廷裔美國數學家格里高列·蔡廷等也作出了一定的貢獻。對於有限項的隨機數列,柯爾莫哥洛夫將它的隨機性定義為“熵”,也就是後來的柯氏複雜性。這個定義下,一個包含了0與1組成的、長度為 的字元串(或者數列,二者並無本質上的區別),其“熵”的大小為這個數列的最短描述的長度和 的接近程度。字元串的複雜度越接近於 ,它也會越隨機;而字元串的複雜性越低於 ,它也就越不隨機。
3.可預測性法
這個方法由德國數學家克勞斯·施諾提出。他用了一個和傳統機率論稍有不同的鞅的定義。他證明了“若人們擁有一個下注策略,可以從多種可能中選擇出最優的方案,那么人們也可以用類似的策略選出一個有偏差的子集。”如果人們只需要一個遞歸性的鞅(而不是構造的方式)便能夠成功選出數列的話,那么人們就該使用遞歸隨機性的概念中。美國數學家Yongge Wang則證明出,遞歸隨機性和施諾的隨機性並不是同一個概念。
這三個方式在大多數情況下被證實是等價的。
需要注意的是,按照以上任意一個關於無限數列的隨機性定義,由於都是著眼於隨機性趨勢,因此對數據開頭部分的隨機性不敏感。如果在隨機數列的第一項前插入哪怕一百萬個0,得出的仍然會是隨機數列。因此,套用這幾個定義時應該小心謹慎。
