概念
鏈復形(chain complex)是一種抽象的復形。設{C}是一族交換群和滿足∂°∂=0的一族同態{:C→C},則由它們組成的C={C,}稱為一個鏈復形。同態∂q稱為鏈復形的邊緣運算元,群C及其子群:
Z(C)=ker∂, B(C)=Im∂
分別稱為鏈復形C的q維鏈群及q維閉鏈群,q維邊緣鏈群,商群H(C)=Z(C)/B(C) (q∈Z)稱為鏈復形C的q維同調群。類似地可定義和討論與鏈復形有關的鏈映射、鏈同倫以及鏈復形的同調序列等同調理論。
從單純同調群和奇異同調群的理論可看出這些對象有許多共同特徵。比如它們都有一系列交換群,以及滿足∂q°∂q+1=0的一系列邊緣同態運算元。為了深入研究同調理論,有必要抽象出這些代數的概念。
上復形
復形常指上復形。上復形亦稱上鏈。一種特殊的模同態序列。設有A-同態序列:
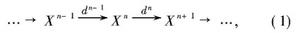 鏈復形
鏈復形這個序列的兩個方向都是無限的,若對每個整數n皆有dd=0,則稱序列(1)為環A上的上復形.把模同態d:X→X稱為上邊緣同態或上邊緣運算元。為簡便起見,用(X,d)代表復形序列(1).如果記X=X,d=d,則序列(1)可以表示為:
且dd=0,把序列(2)稱為環A上的復形或鏈,模同態d稱為邊緣同態或邊緣運算元。
同態
設E與F為兩個群胚,它們的合成法則分別記為⊥與⊤。稱從E到F中的映射f是群胚同態,如果對於E的任一元素偶(x,y),有:
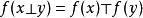 鏈復形
鏈復形設E與F為兩個么半群(兩個群),稱從E到F中的映射。f是么半群(群)的同態,如果f是群胚的同態,且E的中性元素的象是F的中性元素。(在群的情況下,後一個條件是自然滿足的,但是從加法么半群N到乘法么半群N的映射x↦0是群胚的同態, 而並不因此就是么半群的同態)。
設G為乘法群,而a為G的元素。由關係f(n)=an所定義的從加法群Z到G中的映射f是群的同態。
設A與B為兩個環(兩個體),稱從A到B中的映射f是環(體)的同態,如果f是加法群的同態,且為乘法么半群的同態。這就是說,對A的任一元素偶(x,y),有:
f(x+y)=f(x)+f(y)f(xy)=f(x)f(y),
並且f將A的單位元變成B的單位元。
例如,設n為非零自然數;使任一有理整數對應其對模n的剩餘類映射是從環Z到環Z/nZ上的同態。設E與F為兩個A-代數(兩個酉A-代數)。稱從E到F中的映射f是A-代數(酉A-代數)的同態,如果它是線性映射,並且是乘法群胚(乘法么半群)的同態。
例如,設E為交換體K上的非零有限n維向量空間,而B為E的基。則從E的全體自同態之酉代數ℒ(E)到K中元素構成的全體n階方陣之酉代數Mn (K)中的映射,如果該映射使E的任一自同態對應它在基B中的矩陣,則這一映射是酉代數的同態。
同態的概念能用抽象的方式加以推廣。
鏈群
鏈群是建立同調群的重要概念。設K是一個n維復形,它的全體q維單形的集合記為{s|i=1,2,…,α,q=0,1,…,n}。設sq是q維單形s任意選定了一個定向後形成的有向單形,當q=0時,記s=+〈a〉,則這樣的有向單形組:
{s|i=1,2,…,α,q=0,1,2,…,n}
稱為復形K的有向單形的一個基本組。對於整數加群Z中的整數g,約定gs=(-g)(-s),則以整數為係數的任意一個線性組合:
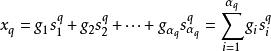 鏈復形
鏈復形稱為K的一個q維鏈;當其係數全為零時,這個鏈用0表示。若另有q維鏈:
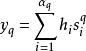 鏈復形
鏈復形定義它們的和為
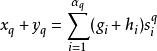 鏈復形
鏈復形則對這樣的加法,K的全體q維鏈形成一個自由交換群,稱為K的q維鏈群,記為C(K;Z),或簡記為C(K)。基本組{s}為這鏈群的一組基。為了方便也可將q推廣到所有整數,當q<0或q>n時,規定C(K)=0。
