對偶空間

對偶空間構造是 行向量(1×n)與列向量(n×1)的關係的抽象化。這個結構能夠在無限維度空間進行並為測度,分布及希爾伯特空間提供重要的觀點。對偶空間的套用是泛函分析理論的一特徵。 傅立葉變換亦內蘊對偶空間的概念。

代數的對偶空間

設V為 在域F上的向量空間，定義其對偶空間V 為由V到F的所有線性函式的集合。 即是V的標量線性變換。V* 本身是Ｆ的向量空間並且擁有加法及標量乘法：

∀ φ, ψ ∈ V*, ∀ a ∈ F , ∀ x ∈ V. 在張量的語言中,V的元素被稱為逆變(contravariant)向量而V*的元素被稱為協變(covariant)向量，同向量(co-vectors)或一形(one-form)。例子

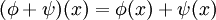
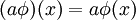
如果V是有維限的,V*的維度和V的維度便相等; 如果{e1,...,en}是V的基，V* 便應該有相對基 {e,...,e}，記作：

如果V 是平面幾何向量的空間，V* 便是一組組的平衡線。我們能從平衡線套用到任何向量產生一個標量。
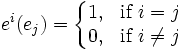
如果V是無限維度，e 不能產生V* 的基;而V* 的維度比V的大。
例如空間R的元素是實數列，其擁有很多非零數字。R的雙對空間是所有實數數列的空間。這些數列(an) 被用於元素(xn) 而產生∑nanxn。線性映射的轉置

設 f: V -> W 是線性映射。 f 的轉置 f : W* → V* 定義為

∀ φ ∈ W*. 對任何向量空間 V,W，定義 L(V,W) 為所有從 V 到 W 的線性映射組成的向量空間。f |-> f 產生從 L(V,W) 至L(W ,V )的單射 ；這是個同構若且唯若 W 是有維限的。
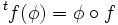
若 線性映射 f 表示作其對 V,W 的基之矩陣 A , 則 f 表示作其對 V ,W 的對偶基之 轉置矩陣。 若 g: W → X 是另一線性映射，則 (g o f) = f o g.
在範疇論的語言裡,為任何向量空間取對偶及為任何線性映射取轉置 都是向量空間範疇的逆變函子。雙線性乘積及對偶空間

正如所見，如果V擁有有限維度，V跟V*是同構的，但是該同構並不自然；它是依賴於我們開始所用的V的基。事實上，任意同構Φ (V → V*) 在V上定義了一個唯一的非退化的雙線性型：

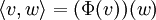
相反地從每個在有限維空間中的非退化的雙線性積可以產生由V映射到V*的同構。到雙對偶空間內的單射

存在一個由V到其雙對偶V**的自然映射Ψ ，定義為
(Ψ(v))(φ) = φ(v) ∀ v ∈ V, φ ∈ V*.
Ψ 常是單射; 若且唯若V的維數有限時, Ψ 是個同構

連續對偶空間

處理拓撲向量空間時，我們一般僅感興趣於該空間射到其基域的 連續線性泛函。由此導致連續對偶空間之概念，此乃其代數對偶空間之一子空間。向量空間 V 之連續對偶記作 V′。此脈絡下可逕稱連續對偶為對偶。
線性賦范向量空間 V （如一巴拿赫空間或一希爾伯特空間）之連續對偶 V′ 產生一線性賦范向量空間。對一 V 上之連續線性泛函，其範數 ||φ|| 定義為

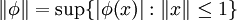
此法變一連續對偶為一線性賦范向量空間，實為巴拿赫空間。例子

對任意有限維之 線性賦范向量空間或拓撲向量空間，正如歐幾里得空間，其連續與代數對偶不二。
令 1 < p < ∞ 為實數，並考慮所有序列 a = (an) 構成之巴拿赫空間 l，使其範數

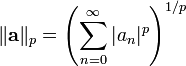
有限。以 1/p + 1/q = 1 定義 q， l 其連續對偶遂自然等同於 l：給定一元素 φ ∈ (l)， l 中相應元素為序列 (φ(en)) ，其中 en 謂第 n 項為 1 且餘項皆 0 之序列。反之，給定一元素 a = (an) ∈ l，l 上相應之連續線性泛函 φ 定為 φ(a) = ∑nanbn （對一切 a = (an) ∈ l）(見 H&ouml;lder不等式)。
準此， l之連續對偶亦自然同構於 l。再者，巴拿赫空間 c （賦以上確界範數之全體收斂序列）及c0（c 中收斂至零者）之連續對偶皆自然同構於 l。進一步的性質

若 V 為希爾伯特空間，則其連續對偶亦然，並反同構於 V；此蓋黎茲表示定理所明，物理學人賴以描述量子力學之bra-ket 符號肇端乎是。
類似雙重代數對偶，對連續線性運算元亦有連續單射 Ψ : V → V ''，此映射實為等距同構，即 ||Ψ(x)|| = ||x|| 對一切 V 中 x 皆真。使 Ψ 為雙射之空間稱自反空間。
連續對偶賦 V 以一新拓撲，名弱拓撲。
若 V 之對偶可分，則 V 亦可分。反之則不然；試取空間 l1，其對偶 l∞ 不可分。