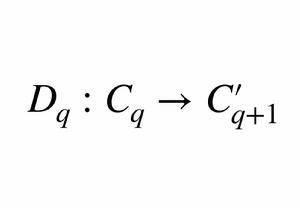定義
鏈同倫是從一個給定的鏈復形的所有鏈映射之間的一種等價關係。
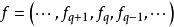 鏈同倫
鏈同倫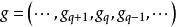 鏈同倫
鏈同倫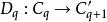 鏈同倫
鏈同倫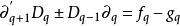 鏈同倫
鏈同倫設 和 是鏈復形(C,∂)到鏈復形(C',∂')的兩個鏈映射。如果有一串同態 使得對任何q都有 則稱鏈同態f和g是鏈同倫的。這一串同態Dq 稱為f和q之間的鏈同倫。
性質
定理
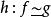 鏈同倫
鏈同倫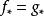 鏈同倫
鏈同倫若有 ,則 。
推論
推論一
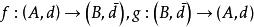 鏈同倫
鏈同倫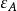 鏈同倫
鏈同倫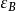 鏈同倫
鏈同倫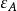 鏈同倫
鏈同倫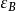 鏈同倫
鏈同倫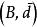 鏈同倫
鏈同倫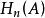 鏈同倫
鏈同倫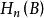 鏈同倫
鏈同倫若 都是復形映射,gf與 同倫,fg與 同倫,這裡 與 相應表示復形(A,d)與 的恆等映射,則 與 同構。
推論二
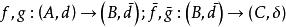 鏈同倫
鏈同倫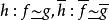 鏈同倫
鏈同倫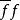 鏈同倫
鏈同倫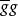 鏈同倫
鏈同倫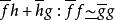 鏈同倫
鏈同倫設 均為復形映射,且 ,則 和 也必同倫,其鏈同倫為 。
鏈同倫等價
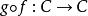 鏈同倫
鏈同倫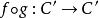 鏈同倫
鏈同倫對於兩個鏈復形(C,∂)和(C',∂'),若存在鏈映射f:C→C'和g:C'→C使得 和 分別鏈同倫等價於C 和C' 的恆同鏈映射,則稱鏈復形(C,∂)和(C',∂')是鏈同倫等價的(chain homotopy equivalent)。
鏈同倫和鏈同倫等價分別是映射的同倫和拓撲空間的同倫等價在鏈復形與鏈映射範疇中的體現。
例如,如果f和g是從拓撲空間X到拓撲空間Y的相互同倫的映射,那么它們導出的從X的奇異鏈復形的鏈映射是鏈同倫的;如果拓撲空間X和Y是同倫等價的,那么它們的奇異鏈復形是鏈同倫等價的。