概念
單純鏈映射(simplicial chain map)是由單純映射決定的鏈映射。設f:K→L是一個單純映射,定義同態如下:
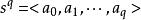 單純鏈映射
單純鏈映射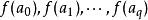 單純鏈映射
單純鏈映射1.若 是K的一個有向單形,當 不相同時,記:
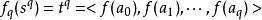 單純鏈映射
單純鏈映射當存在f(a)=f(a)且i≠j時,記f(s )=0。
2.對於任意鏈x=∑gs∈C(K),記:
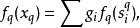 單純鏈映射
單純鏈映射當q<0或q>dim K時,規定f=0;則這一系列同態:
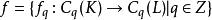 單純鏈映射
單純鏈映射是鏈映射,並把f={f}稱為單純鏈映射(詳細地,是由單純映射誘導的鏈映射),這裡仍用f記單純映射f誘導的鏈映射,一般不會引起混淆。
單純映射
單純映射聯繫復形的多面體之間的一類重要映射。它是從復形K的多面體|K|到復形L的多面體|L|的連續映射,任何連續映射在某種意義下可用它逼近。設K和L是兩個復形,f:|K|→|L|是映射,若它滿足條件:
1.對於任意頂點a∈K ,有f(a)∈L (即L的頂點)。
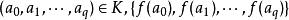 單純鏈映射
單純鏈映射2.對於任意單形是L中某單形的頂點集(可能有重複)。
3.對於任意(a,a,…,a)∈K,
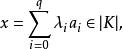 單純鏈映射
單純鏈映射有:
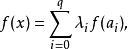 單純鏈映射
單純鏈映射則稱f為單純映射,也可簡記為f:K→L(省去多面體|K|,|L|的記號)。單純映射是連續映射;單純映射由限制在頂點集上的映射:
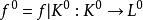 單純鏈映射
單純鏈映射完全決定。反之,對於頂點集之間的任意映射f ,只要f 把K中任意單形的頂點集映成L中某單形的頂點集,它就惟一地確定一個單純映射f:K→L。
映射
在數學裡,映射是個術語,指兩個元素的集之間元素相互“對應”的關係,為名詞。映射,或者射影,在數學及相關的領域經常等同於函式。 基於此,部分映射就相當於部分函式,而完全映射相當於完全函式。
兩個非空集合A與B間存在著對應關係f,而且對於A中的每一個元素x,B中總有有唯一的一個元素y與它對應,就這種對應為從A到B的映射,記作f:A→B。其中,b稱為元素a在映射f下的象,記作:b=f(a)。a稱為b關於映射f的原象。集合A中所有元素的象的集合稱為映射f的值域,記作f(A)。
或者說,設A,B是兩個非空的集合,如果按某一個確定的對應關係f,使對於集合A中的任意一個元素x,在集合B中都有唯一的元素y與之對應,那么就稱對應f:A→B為從集合A到集合B的一個映射。
映射,或者射影,在數學及相關的領域還用於定義函式。函式是從非空數集到非空數集的映射,而且只能是一對一映射或多對一映射。
映射在不同的領域有很多的名稱,它們的本質是相同的。如函式,運算元等等。這裡要說明,函式是兩個數集之間的映射,其他的映射並非函式。一一映射(雙射)是映射中特殊的一種,即兩集合元素間的唯一對應,通俗來講就是一個對一個(一對一)。
注意:(1)對於A中不同的元素,在B中不一定有不同的象;(2)B中每個元素都有原象(即滿射),且集合A中不同的元素在集合B中都有不同的象(即單射),則稱映射f建立了集合A和集合B之間的一個一一對應關係,也稱f是A到B上的一一映射。
鏈映射
鏈映射是聯繫復形的鏈群之間的一種系列同態。為了使復形的鏈群之間的同態能誘導出同調群之間的同態,因而它應將閉鏈與邊緣鏈分別映成閉鏈與邊緣鏈。設K與L都是復形,
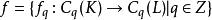 單純鏈映射
單純鏈映射是一系列同態,若滿足條件:°f=f°,則稱f={f}為從K到L的鏈映射。它可理解為下圖具有交換性,即鏈映射具有將閉鏈映為閉鏈和將邊緣鏈映為邊緣鏈的性質,因此它誘導出同調群之間的一系列同態:
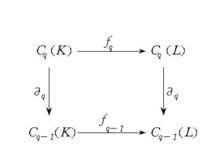 單純鏈映射
單純鏈映射稱為鏈映射f的誘導同態。同時具有性質,若:
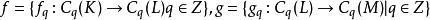 單純鏈映射
單純鏈映射為鏈映射,則複合映射:
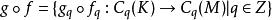 單純鏈映射
單純鏈映射也是鏈映射,並且誘導同態:
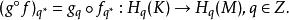 單純鏈映射
單純鏈映射這些概念可推廣到係數群為任意交換群G的情形。
