簡介
解薛丁格方程的一種常用的近似方法。一個量子體系，如果總哈密頓量的各部分具有不同的數量級，又對於它精確求解薛丁格方程有困難，但對於哈密頓量的主要部分可以精確求解,便可先略去次要部分,對簡化的薛丁格方程求出精確解；再從簡化問題的精確解出發，把略去的次要部分對系統的影響逐級考慮進去，從而得出逐步接近於原來問題精確解的各級近似解。這種方法稱為微擾論。
具體方法
對於哈密頓量不顯含時間的體系,其不含時間的薛丁格方程為
(1)
量子力學的微擾論如果<
(2)
量子力學的微擾論
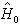量子力學的微擾論
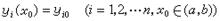量子力學的微擾論
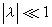量子力學的微擾論 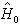量子力學的微擾論其中為未受微擾的哈密頓算符(主要部分)，為微擾項（次要部分），，λ是用來表示微擾強度特徵的小參數。若的本徵方程
(3)
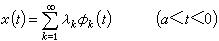量子力學的微擾論
量子力學的微擾論
量子力學的微擾論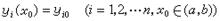 量子力學的微擾論已解出，是未受微擾體系的能量,是與之相應的波函式。當考慮到的作用後,體系的能量與波函式將發生微小變化,此變化依賴於參數λ，於是體系能量和波函式可按λ的冪次作微擾展開
(4)
(5)
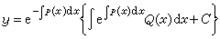量子力學的微擾論
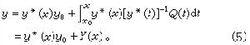量子力學的微擾論
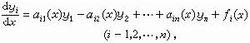量子力學的微擾論 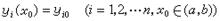量子力學的微擾論
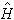量子力學的微擾論當λ=0時,顯然有 ,且=，=。將式(4)、(5)代入式(1)，按λ冪次得到一系列確定、，、,…的等式。實際上λ的冪次標誌著數量級的大小,依次地，、分別為、的零級近似能量和波函式,它們已由式(3)解出，由零級近似解以及 ，可進一步得到能量和波函式一級修正值和,也就是得到了、的一級近似解+、+，以此類推，可逐級求出高級近似解。計算表明，準確到(=1，2,…)級近似的能量等於對於歸一化的第-1級近似波函式下的平均值。以上是定態微擾論的物理思想。
當體系的哈密頓量顯含時間時,體系無確定能量,只要求波函式的近似解，處理問題的基本思想與定態微擾論相同，所不同的是將解不含時間的薛丁格方程改為解含時間的薛丁格方程。這種微擾論是含時間的微擾論。微擾論的具體形式雖是多種多樣的，但都體現了這樣一個特點：微擾項對未受微擾體系的解影響很小，可以通過逐級近似求解。
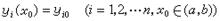量子力學的微擾論 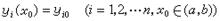量子力學的微擾論利用微擾論處理實際問題時,如果較小得多,使得微擾展開式收斂得較快，就只要計算一、二級微擾便可得到較為滿意的結果。量子力學中的微擾論廣泛地套用於原子和分子物理學中，它常與量子力學的變分法等近似方法結合起來使用。
