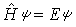量子力學的變分法

解薛丁格方程的一種套用範圍極廣的近似方法。對於束縛定態，它是基於能量本徵值方程（即不含時間的薛丁格方程）與能量變分原理的等價性，通過求能量的極值得到能量本徵值方程的解。

在處理具體問題時，總是採用波函式某種特殊的變化去代替最普遍的任意變分，這樣就可得到依賴于波函式特殊形式的近似解。這種方法稱為變分法。若體系的哈密頓量算符為彑，其能量本徵值方程為

, (1)

量子力學的變分法

該體系的能量平均值

(2)

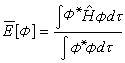量子力學的變分法

量子力學的變分法

是波函式的泛函。式中表示對體系全部坐標積分。可以證明，求彑的本徵值方程，等價於求解

(3)

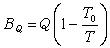量子力學的變分法

也就是滿足變分原理(3)的為彑的本徵函式,唕的極值為所對應的本徵值，即

(4)

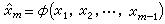量子力學的變分法

這樣，如果能猜測到一個正好滿足式(1),則由式(2)所得的唕【】等於，如果猜測的與略有不同,則唕【】必定大於，因而唕【】總是給出唕的一個上限。當做了多次猜測之後,其中最小的唕一定是這些猜測中最好的，這樣就把最小的唕取作E的近似值。套用以上手續可得到一種通過猜測去計算能量近似值的方法。改善波函式通常是通過一個含連續參數的特殊形式的波函式(,,,,…)來實現的，這樣唕也就是這些參數的函式。式中代表體系的全部坐標，所猜測的波函式(,,,,…)稱為嘗試波函式,變分參數(,,,…)是待定的。根據變分原理，由唕取極值，則有

(5)

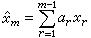量子力學的變分法

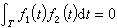量子力學的變分法

通過以上方程組可解得(i=1,2,3,…)，於是(,嬼,嬽,嬿,…)和(嬼,嬽,嬿,…)分別是和在(,,,,…)形式下最好的近似。它的近似性來源於用參數的變化代替了普遍形式的任意變分、顯然，參數愈多,嘗試波函式的變化愈普遍,所得結果愈好。在選取嘗試波函式時,要注意使其與滿足相同的邊界條件。
如果嘗試波函式與精確解的差為量級,則唕與精確解的差為||量級，因而即使用粗糙的嘗試波函式也可得到近似性很好的能量本徵值。通常用這種方法求體系基態能量的近似值。考慮到不同能量的本徵函式彼此正交,也可以由低至高逐級求激發態能量的近似值,其近似性較基態為差。變分法的優點在於運用它求解不受什麼限制，但是由於結果的好壞完全取決於嘗試波函式的選擇，致使結果的任意性大。以上是解束縛定態的變分法。
對於散射問題，如將決定能量的變分原理改為決定相移的變分原理，以上方法的基本思想仍適用。變分法也常與量子力學的微擾論結合起來使用。