定義式
| 銳角三角函式 | 任意角三角函式 | |
|---|---|---|
| 圖形 |  直角三角形 直角三角形 |  任意角三角函式 任意角三角函式 |
| 正弦 (sin) | | |
| 餘弦 (cos) | | |
| 正切 (tan或tg) | | |
| 餘切 (cot或ctg) | | |
| 正割 (sec) | | |
| 餘割 (csc) | | |
表格參考資料來源:現代漢語詞典.
相關概念
相關概念三角函式的標準英文讀音音
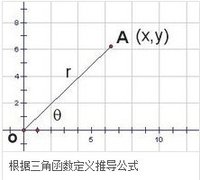 三角函式公式
三角函式公式正弦:sine(簡寫sin)[sain]
餘弦:cosine(簡寫cos)[kəusain]
正切:tangent(簡寫tan)['tændʒənt]
餘切:cotangent(簡寫cot)['kəu'tændʒənt]
正割:secant(簡寫sec)['si:kənt]
餘割:cosecant(簡寫csc)['kau'si:kənt]
正矢:versine(簡寫versin)['və:sain]
余矢:versed cosine(簡寫vercos)['və:sə:d][kəusain]
直角三角函式
直角三角函式 (∠α是銳角)
三角關係
倒數關係:cotα*tanα=1
商的關係:sinα/cosα=tanα
平方關係:sin²α+cos²α=1
誘導公式
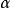 三角函式公式
三角函式公式公式一:設
為任意角,終邊相同的角的同一三角函式的值相等:
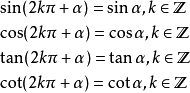 三角函式公式
三角函式公式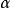 三角函式公式
三角函式公式公式二:設
為任意角,
與
的三角函式值之間的關係:
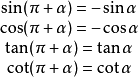 三角函式公式
三角函式公式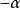 三角函式公式
三角函式公式公式三:任意角
與
的三角函式值之間的關係:
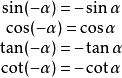 三角函式公式
三角函式公式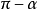 三角函式公式
三角函式公式公式四:
與
的三角函式值之間的關係:
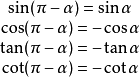 三角函式公式
三角函式公式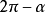 三角函式公式
三角函式公式公式五:
與
的三角函式值之間的關係:
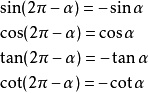 三角函式公式
三角函式公式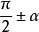 三角函式公式
三角函式公式公式六:
及
與
的三角函式值之間的關係:
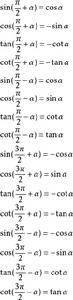 三角函式公式
三角函式公式記背訣竅:奇變偶不變,符號看象限.
基本公式
和差角公式
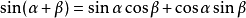 三角函式公式
三角函式公式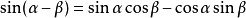 三角函式公式
三角函式公式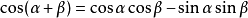 三角函式公式
三角函式公式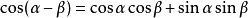 三角函式公式
三角函式公式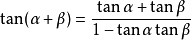 三角函式公式
三角函式公式 三角函式公式
三角函式公式證明如圖,負號的情況只需要用-β代替β即可.cot(α+β)推導只需把角α對邊設為1,過程與tan(α+β)相同.
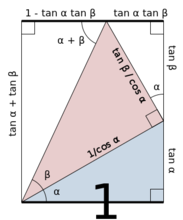 證明正切的和差角公式
證明正切的和差角公式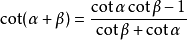 三角函式公式
三角函式公式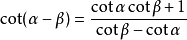 三角函式公式
三角函式公式 三角函式公式
三角函式公式 三角函式公式
三角函式公式和差化積
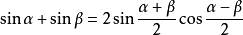 三角函式公式
三角函式公式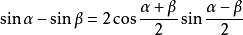 三角函式公式
三角函式公式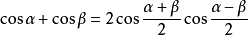 三角函式公式
三角函式公式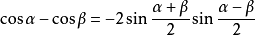 三角函式公式
三角函式公式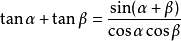 三角函式公式
三角函式公式口訣:正加正,正在前,余加余,余並肩,正減正,余在前,余減余,負正弦.
積化和差
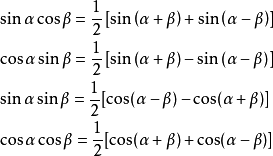 三角函式公式
三角函式公式倍角公式
二倍角公式
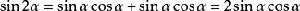 三角函式公式
三角函式公式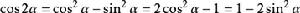 三角函式公式
三角函式公式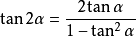 三角函式公式
三角函式公式三倍角公式
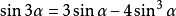 三角函式公式
三角函式公式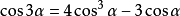 三角函式公式
三角函式公式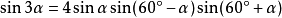 三角函式公式
三角函式公式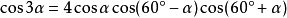 三角函式公式
三角函式公式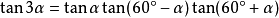 三角函式公式
三角函式公式證明
:
sin3a
=sin(a+2a)
=sin2acosa+cos2asina
=2sina(1-sin^2a)+(1-2sin^2a)sina
=3sina-4sin^3a
cos3a
=cos(2a+a)
=cos2acosa-sin2asina
=(2cos^2a-1)cosa-2(1-cos^2a)cosa
=4cos^3a-3cosa
sin3a
=3sina-4sin^3a
=4sina(3/4-sin^2a)
=4sina[(√3/2)-sina][(√3/2)+sina]
=4sina(sin60°+sina)(sin60°-sina)
=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°+a)/2]
=4sinasin(60°+a)sin(60°-a)
cos3a
=4cos^3a-3cosa
=4cosa(cos^2a-3/4)
=4cosa[cos^2a-(√3/2)^2]
=4cosa(cosa-cos30°)(cosa+cos30°)
=4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°)/2]}
=-4cosasin(a+30°)sin(a-30°)
=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]
=-4cosacos(60°-a)[-cos(60°+a)]
=4cosacos(60°-a)cos(60°+a)
上述兩式相比可得:
tan3a=tanatan(60°-a)tan(60°+a)
四倍角
sin4A=-4*(cosA*sinA*(2*sinA^2-1))
cos4A=1+(-8*cosA^2+8*cosA^4)
tan4A=(4*tanA-4*tanA^3)/(1-6*tanA^2+tanA^4)
五倍角
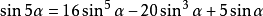 三角函式公式
三角函式公式 三角函式公式
三角函式公式 三角函式公式
三角函式公式n
 三角函式公式
三角函式公式套用歐拉公式:
.
上式用於求n倍角的三角函式時,可變形為:
 三角函式公式
三角函式公式所以,
 三角函式公式
三角函式公式其中,Re表示取實數部分,Im表示取虛數部分.而
 三角函式公式
三角函式公式所以,
 n倍角的三角函式
n倍角的三角函式半角公式
 三角函式公式
三角函式公式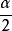 三角函式公式
三角函式公式(正負由
所在的象限決定)
萬能公式
 三角函式公式
三角函式公式輔助角公式
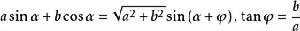 三角函式公式
三角函式公式.
證明:
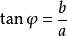 三角函式公式
三角函式公式由於
,顯然
,且
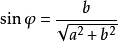 三角函式公式
三角函式公式 三角函式公式
三角函式公式故有:
 三角函式公式
三角函式公式三角形定理
正弦定理
詳見詞條:正弦定理
在任意△ABC中,角A、B、C所對的邊長分別為a、b、c,三角形外接圓的半徑為R.則有
:
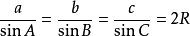 三角函式公式
三角函式公式正弦定理變形可得:
 三角函式公式
三角函式公式餘弦定理
詳見詞條:餘弦定理
在如圖所示的在△ABC中,有
 三角函式公式
三角函式公式或
 三角函式公式
三角函式公式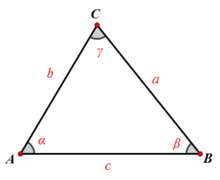 餘弦定理
餘弦定理三角函式的套用
在海島A上有一座海拔1千米的山,山頂設有一個觀察站P,上午11時,測得一輪船在海島北偏東30,俯角為30的B處。到11時10分又測得該船在島北偏西60,俯角為60的C處。(1)該船的航行速度是每小時多少千米?(2)又經過一段時間後,船到達海島正西方向的D處,此時船距島A有多遠?
解(1)在Rt△PAB中,∠APB=60° PA=1,∴AB=√ 3(千米) 在Rt△PAC中,∠APC=30°,∴AC=√ 3/3(千米)在△ACB中,∠CAB=30°+60°=90°則BC=√ (AB)^2+(AC)^2=√ (√ 3/3)^2+(√ 3)^2=√ 30/3(√ 30/3)/(1/6)=2√ 30(千米/時)(2)∠DAC=90°-60°=30°sinDCA=sin(180°-∠ACB)=sinACB=AB/BC=√ 3/√ 30/3=3√ 10/10sinCDA=sin(∠ACB-30°)=sinACB·cos30°-cosACB·sin30°=(3√ 3-1)√ 10/20在△ACD中,據正弦定理得,AD/sinDCA=AC/sinCDA∴AD=ACsinCDA/sinDCA=(9+√ 3)/13答:此時船距島A為(9+√ 3)/13千米.
