歷史
1920年代後期,數學家大衛·希爾伯特的學生Gabriel Sudan和威廉·阿克曼,當時正研究計算的基礎。Sudan發明了一個遞歸卻非原始遞歸的Sudan函式。1928年,阿克曼又獨立想出了另一個遞歸卻非原始遞歸的函式。[1]
他最初的念頭是一個三個變數的函式A( m, n, p),使用康威鏈式箭號表示法是 m→ n→ p。阿克曼證明了它是遞歸函式。希爾伯特在 On the Infinite猜想這個函式不是原始遞歸函式。阿克曼在 On Hilbert's Construction of the Real Numbers證明了這點。
後來Rózsa Péter和拉斐爾·米切爾·羅賓遜定義了一個類似的函式,但只用兩個變數。
定義
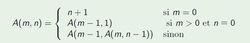 阿克曼函式
阿克曼函式Ackermann函式定義如下: 若m=0,返回n+1。
若m>0且n=0,返回Ackermann(m-1,1)。
若m>0且n>0,返回Ackermann(m-1,Ackermann(m,n-1))。
意義
從Ackermann函式的定義中可以看出,Ackermann函式可以看成關於n的一個函式序列,其中第0個函式返回n+1,而第m個函式則是將第m-1個函式對1疊代n+1遍。對較小的m,該函式為:
Ackermann(0,n)=n+1
Ackermann(1,n)=n+2
Ackermann(2,n)=2*n+3
Ackermann(3,n)=2^(n+3)-3
Ackermann(4,n)=2^2^2^……^2-3,乘冪中共有n+3個2。
當m≥4,Ackermann函式的增長快得驚人。Ackermann(4,0)=13,Ackermann(4,1)=65533,Ackermann(4,2)=2^65536-3有19729位,而Ackermann(4,3)則即使是位數也不易估計。Ackermann(5,0)=65533,Ackermann(5,1)=Ackermann(4,65533)……
反函式
單變數反Ackermann函式(簡稱反Ackermann函式)α(x)定義為最大的整數m使得Ackermann(m,m)≤x。從上面的討論中可以看到,因為Ackermann函式的增長很快,所以其反函式α(x)的增長是非常慢的,對所有在實際問題中有意義的x,α(x)≤4,所以在算法時間複雜度分析等問題中,可以把α(x)看成常數。
α(x)出現在使用了按秩合併和路徑壓縮的並查集算法的時間複雜度中。
計算代碼
遞歸算法
int ack(int m,int n){
while(m!=0){
if( n==0) n=1;
else{
n=ack(m, n-1);}
m--;
}
return n+1;
}
非遞歸算法一
int Ackermann(int m,int n)
{
int akm[m][n];
int i,j;
memset(akm,o,sizeof(akm));
for(j=0;j<n;j++)
akm[0][j]=j+1;
for(i=1;i<m;i++)
{
akm [0]=akm[i-1][1];
for(j=1;j<n;j++)
{
akm[j]=akm[i-1][akm [j-1]];
}
}
return akm[m][n];
}
非遞歸算法二
stack s;
int ack(int m,int n)
{
int top=0;
s[top].mval=m;
s[top].nval=n;
do
{
while(s[top].mval)
{
while(s[top].nval)
{
top++;
s[top].mval=s[top-1].mval;
s[top].nval=s[top-1].nval-1;
}
s[top].mval--;
s[top].nval=1;
}
if(top>0)
{
top--;
s[top].mval--;
s[top].nval=s[top+1].nval+1;
}
}while(top!=0||s[top].mval!=0);
ack=s[top].nval+1;
top--;
}

