什麼是逆向歸納法
逆向歸納法(backward induction)是求解動態博弈均衡的方法。所謂動態博弈是指博弈參與人的行動存在著先後次序,並且後行動的參與人能夠觀察到前面的行動。逆向歸納法在邏輯上是嚴密的,然而它存在著“困境”。所謂逆向歸納法是從動態博弈的最後一步往回推,以求解動態博弈的均衡結果。逆向歸納法又稱逆推法。它是完全歸納推理,其推理是演繹的,即結論是必然的。
在完全且完美的動態博弈中,先行為的理性博弈人,在前面階段選擇策略時,必然會考慮後行博弈人在後面階段中將會怎樣選擇策略。因而,只有在博弈的最後一個階段,不再有後續階段牽制的情況下,博弈人才能作出明智的選擇。在後面階段博弈人選擇的策略確定後,前一階段的博弈人在選擇策略時也就相對容易。
逆向歸納法就是從動態博弈的最後一個階段開始分析,逐步向前歸納出各階段博弈人的選擇策略。
逆向歸納法的邏輯基礎:動態博弈中先行動的參與人,在前面階段選擇行為時必然會考慮後行動的參與人在後面階段中的行為選擇,只有在最後一階段的參與人才能不受其他參與人的制約而直接做出選擇。而當後面階段的參與人的選擇確定後,前一階段的參與人的行為也就容易確定了。逆向歸納法排除了不可信的威脅或承諾。
歷史
逆向歸納法是博弈論中一個比較古老的概念,它的提出最早可以追溯到澤梅羅(1913) 針對西洋棋有最優策略解的證明,後來人們將其推廣到了更廣泛的博弈中,例如,在有限完美信息擴展型博弈中,就是用逆向歸納法(BI)來證明子博弈完美均衡(SPE)的存在以 及求解 SPE,其基本思路是從動態博弈中的最後一個階段開始,局中人都遵循效用最大化原則選擇行動,然後逐步倒推至前一個階段,一直到博弈開始局中人的行動選擇,其邏輯嚴密性毋庸置疑。然而,當從終點往前推到某一決策點時,BI 完全忽略了到達該決策點的以往歷史行動,而這一歷史行動當然會影響處於該決策點的局中人有關其對手將來如何採取行動的信念,例如,一個局中人如果觀察到對手在過去沒有按照 BI 進行行動選擇,那么他就有理由相信他的對手仍會採取同樣的模式進行下去,但是通過這種信念修正以後所做的選擇就會與 BI矛盾。為了達到均衡解,為了能按 BI進行推理求解,我們需要對局中人的信念或者說知識增加一些限制性條件,也就是說在什麼樣的前提下,BI 是合理的,顯然,僅僅要求每個局中人都理性是不夠的,所有的局中人都必須知道所有的局中人都是理性的,所有的局中人都必須知道所有局中人都知道所有局中人都是理性的……等等以至無窮,在這樣的認知條件基礎下,我們就不會偏離 BI,即, “在完美信息擴展型博弈中,理性的公共知識蘊含了BI”(Aumann 1995)。
運用
 逆向歸納法
逆向歸納法逆向歸納法:它的精髓就是“向前展望,向後推理”,即首先仔細思考自己的決策可能引起的所有後續反應,以及後續反應的後續反應,直至博弈結束;然後從最後一步開始,逐步倒推,以此找出自己在每一步的最優選擇。
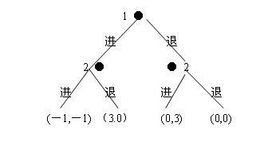
圖的求解過程如下:
(a)若2在右,2將選擇進(0.3);∵(0.3)>(0.0)
(b)若2在左,2將選擇退(3.0);∵(3.0)>(-1.-1)
(c)在2的選擇中1的最大收益是選擇進;∵(3.0)>(0.3)
∴納什均衡為(進(進,退))均衡解為(進,退),均衡收益為(3.0)
逆向歸納法僅適合有限步動態博弈,而且要求決策者犯錯的可能性很小。
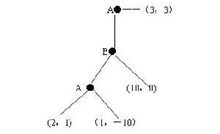
如果使用逆向歸納法得到的結果是A選擇右邊的行動,雙方各得3。
如果A在第一步選擇下邊的行動,B該做何想?只有當A在第二步犯錯誤的可能性小於1/11時,B才有膽量選擇讓遊戲繼續玩下去。於是A極有可能獲得10這個最大回報。
盤點各博弈論
| 博弈論(Game Theory),有時也稱為對策論,或者賽局理論,是研究具有鬥爭或競爭性質現象的理論和方法,它是套用數學的一個分支,既是現代數學的一個新分支,也是運籌學的一個重要學科。 |