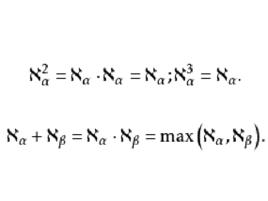基本介紹
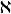 超限基數
超限基數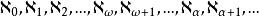 超限基數
超限基數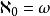 超限基數
超限基數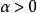 超限基數
超限基數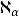 超限基數
超限基數超限基數(transfinite cardinal number)亦稱 無限基數,是一類常見的基數,指與有限基數相對的一類基數,可數基數、不可數基數統稱 超限基數,超限基數又稱為阿列夫()。將所有超限基數從小到大排列出來 ,得到 正則超限基數序列:,是一個無限上升的良序鏈,這裡是可數基數,也是最小的超限基數。當時,都是不可數基數 。
超限基數的性質
有下列性質:
 超限基數
超限基數 超限基數
超限基數1. 對任何基數,都存在比它更大的基數,即
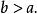 超限基數
超限基數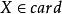 超限基數
超限基數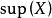 超限基數
超限基數2. 若,則是一個基數。
 超限基數
超限基數3. 超限基數等冪定理:對任何序數,
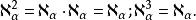 超限基數
超限基數 超限基數
超限基數 超限基數
超限基數4.對任何序數與,
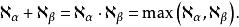 超限基數
超限基數 超限基數
超限基數 超限基數
超限基數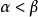 超限基數
超限基數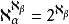 超限基數
超限基數5.對任何序數與, 當時,。
 超限基數
超限基數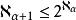 超限基數
超限基數6.對任何序數,。
基數
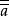 超限基數
超限基數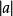 超限基數
超限基數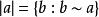 超限基數
超限基數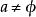 超限基數
超限基數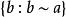 超限基數
超限基數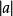 超限基數
超限基數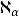 超限基數
超限基數 超限基數
超限基數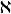 超限基數
超限基數 超限基數
超限基數 超限基數
超限基數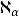 超限基數
超限基數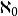 超限基數
超限基數 超限基數
超限基數 超限基數
超限基數基數(cardinal numbers)是集合論基本概念之一。是通常個數概念的推廣。按康托爾原意,集合a的基數是一切與a一一對應的集合的共同特徵,它既捨棄了a中元素的具體屬性,也不考慮a的元素間的次序關係,所以集a的基數是抽象的結果,用a上加兩劃(或)來表示。弗雷格把a的基數定義為所有與a一一對應的集所成之集,即。在ZFC系統中能證明當時,並不構成一個集,而是一個真類。1928年數學家馮·諾伊曼建議選取一個特殊的與a一一對應的集作為a的基數,即把定義為所有與a一一對應的序數中最小的一個。根據集合的良序化定理,與a一一對應的序數是一定存在的,由於序數類的良序性,所有與a一一對應的序數中必有最小的一個,因此任何集合均有基數,並且兩個集合具有相同基數的充要條件就是它們能夠一一對應,這符合康托爾的原意。因為集合有有限、無限之分,相應地,基數亦有有限、超限之分, 有限基數就是自然數;超限基數記作,表示第個超限基數,其中讀作阿列夫,是一個序數。按照的隸屬情況,超限基數亦可分為三類:第一類只含一個基數,它是可數集的基數;當為後繼序數或極限序數時,分別稱為後繼基數與極限基數,它們分別構成第二類與第三類超限基數 。