簡介
艾普塞朗數並不能透過較小序數有限次數的加法及乘法運算而獲得。康托爾原來引進的 艾普塞朗數，乃以以下的方式定義:
ε乃是一個滿足以下式的序數，當中ω乃是最小的無限序數。
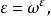艾普塞朗數滿足上式的所有ε當中，最小的記為 ε。它可以透過以下的超限遞歸法獲得:-
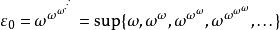艾普塞朗數其後如此類推，
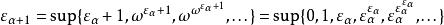艾普塞朗數更大的 艾普塞朗數為
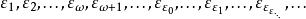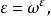艾普塞朗數 艾普塞朗數值得留意的是，ε的基數，仍然為可數的。實際上，所有指標為可數的ε，其基數也是可數的。不可數的ε（意指滿足定義式 的ε）存在，但其指標也是不可數的。
超限序數
超限數是大於所有有限數（但不必為絕對無限）的基數或序數，分別叫做超窮基數（英語：transfinite cardinal number）和超窮序數（英語：transfinite ordinal number）。術語“超限”（transfinite）是康托爾提出的，他希望避免詞語無限（infinite）和那些只不過不是有限（finite）的那些對象有關的某些暗含。當時其他的作者少有這些疑惑；現在被接受的用法是稱超限基數或序數為無限的。但是術語“超限”仍在使用。
超窮序數可以確定超窮基數，並導出阿列夫數序列。
對於有限數，有兩種方式考慮超限數，作為基數和作為序數。不像有限基數和序數，超限基數和超限序數定義了不同類別的數。
1.最小超限序數是ω。
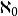艾普塞朗數
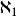艾普塞朗數2.第一個超限基數是aleph-0，整數的無限集合的勢。如果選擇公理成立，下一個更高的基數是aleph-1。如果不成立，則有很多不可比較於aleph-1並大於aleph-0的其他基數。但是在任何情況下，沒有基數大於aleph-0並小於aleph-1。
連續統假設聲稱在aleph-0和連續統（實數的集合）的勢之間沒有中間基數：就是說，aleph-1是實數集合的勢。已經在數學上證實了連續統假設不能被證明為真或假，由於不完備性的影響。
某些作者，比如Suppes、Rubin使用術語超限基數來稱呼戴德金無限集合的勢，在可以不等於無限基數的上下文中；就是說在不假定可數選擇公理成立的上下文中。給定這個定義，下列是等價的：
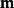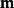艾普塞朗數 艾普塞朗數是超限基數。就是說有一個戴德金無限集合A使得A的勢是。
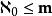艾普塞朗數。
艾普塞朗數。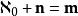
艾普塞朗數
艾普塞朗數有一個基數使得。
