背景
集合論的創建者Cantor驚人的創造了超限基數與超限序數。對於有限集合來說，基數就是這集合中元素的個數。對於無窮的集合，要引進新的基數。自然數集合的基數用(阿列夫0)表示。集合的基數有時也稱為集合的勢或集合的蘊度。可列集的基數通常記作(阿列夫0)，用a表示。與實數集R1對等的集的基數又稱為連續基數或連續勢，用c表示。Cantor還定義了兩個基數的和、乘積和乘冪，其中。諸無限集所具有的基數遠非僅僅a與c。
概念
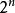連續統基數實直線的基數是。在連續統假設下2是第一個大於叢的基數，記為W，其倍數都表示連續統的基數。在連續統假設下，連續統基數也是不可數基數中最小的一個 。
性質
連續統基數具有下列性質 :
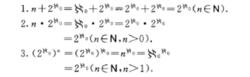連續統的性質連續統與連續統基數在概念上是有區別的，連續統的基數是2式，但具有2式基數的集合不一定是實直線.具有連續統基數的集合很多，例如：
1.n維空間中所有點的集合.
2.所有複數的集合.
3.所有自然數的無窮序列的集合.
4.所有實數的無窮序列的集合.
5. R-A,R是實數集，A是R的任一可數子集.
6.所有無理數的集合.
7.所有自然數的無窮子集的集合.
8.所有N到N的雙射的集合.
9.所有R到R的連續函式的集合.
10.所有實數的開集的集合.
