基本介紹
定義1 (1) 若存在φ:A↦B,對任意x∈A,存在唯一的y∈B,使得y=φ(x);反之,若存在ψ:B↦A,對任意x∈B,存在唯一的y∈A,使得y= ψ(x),則稱A,B是 一一對應的(one-to-one)；
(2)若兩個集A,B是一一對應的,則稱A, B是對等的(equipotent),即A,B有相同基數，記為cardA = cardB。
例如，正奇數集O= {1,3,... ,2n-1,..}和正偶數集E= {2,4,...,2n,..}之間可建立一一對應的關係：
φ:O↦E
使得：
φ(2n- 1)= 2n，
故O和E有相同基數。
又如,O= {1,3,... ,2n-1,...}和正整數集之間可建立一一對應的關係:
φ:O↦Z
使得：
φ(2n- 1)=n
故它們是對等的，這是局部與整體對等的例子。
定義2 (1) 正整數集的基數稱為 可數基數(countable cardinal),記為
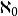可數基數cardZ = 。
(2)若集A與正整數集是對等的，則稱其為 可數的，記為
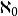可數基數cardA= ，
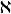可數基數式中: 為猶太人使用的希伯萊文的第一個字母，讀做aleph 。
相關性質
可數集的特徵是其全部元可排成序列 。
下面介紹可數集的幾個重要性質。
定理1 任意無限集都有可數子集。
證 設M是無限集，取e∈M.由於M的無限性，M\{e}是非空的,故可取e∈M\{e}.
一般地，設已選出{e,e,... ,e}.還由於M的無限性，M\{e,e,... ,e}是非空的。繼續選e∈M \{e,e,... ,e}.
由歸納法得可數子集{e,e,... ,e}。證完。
定理1說明可數集是最小的無限集。
定理2 可數集的無限子集是可數的.
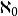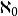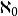可數基數 可數基數 可數基數證 設M是可數集，則cardM=.設M是M的無限子集.由定理1可知，M有可數子集M,即cardM=,所以cardM=，證完。
定理3 有限多個可數集的並是可數的 。
證 設有可數集A,A,...,A,其中
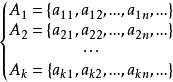可數基數於是，可將可數集A,A,...,A並的元排列成序列:
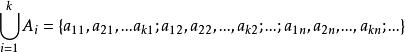可數基數它可與正整數集一一對應， 故是可數的。證完。
進一步還有下述結果。
定理4可數個可數集的並是可數的。
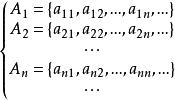可數基數證設有可數集A,A,...,A,...,其中並按下標之和的順序來排列(下標之和是相同的元按第一個下標來排列),於是，
可將A,A,...,A,...並的元排成序列
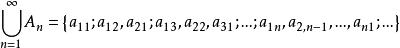可數基數它可與正整數集一一對應，故是可數的。證完 。
例題解析
下面利用上述定理來證明有理數的可數性。
【例1】有理數集(set of rational numbers) Q是可數的。
事實上，設
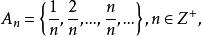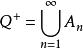可數基數
可數基數則集A是可數的，而正有理數集,故由上述定理可知，正有理數集是可數的。
同理，負有理數集Q 是可數的，故有理數集是可數的 。
