非線性方程
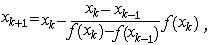非線性方程數值解法nonlinear equation，numerical method of當f（x）是超越函式或高次多項式時，f（x）=0稱為非線性方程，此類方程除少數情形外，只能求近似解。求解非線性方程的主要方法是疊代法。使用這一方法一般至少要知道根的一個近似值x0，然後將原方程f（x）=0改變成與它同解但便於疊代的形式x=j（x），利用疊代公式xk+1=j（xk），k=0，1，2，……就能求出一系列逐步精確的近似值。例如常用的疊代法有：①牛頓疊代公式：
k=0，1，2，……式中x0為初始近似值。②割線疊代公式：k=0，1，2，……式中x0，x1為兩個初始近似值。
詳情
此外還有二次插值法、切比雪夫疊代法及艾特肯加速法等。評價一個疊代公式的優劣，除去收斂條件之外，主要是看它的效能指標，即達到規定的精確度所花費的代價。因此如何構造收斂的疊代公式，分析公式的收斂速度和收斂條件，以及加快收斂的技術，這些都是疊代法研究的課題。牛頓疊代具有較高的收斂速度和簡單靈活等優點，而且可以推廣到求解非線性方程組，擬牛頓法就是具有較高效能指標的求解非線性方程組的通行方法。
非線性方程以高精度算術為支持，可以差商型導數為指導，可計通用求解方法。
二次插值法也是高效的逼近方法，可以將非單調區間割分成單調區間，再高速逼近，其收斂速度明顯高於牛頓法。
