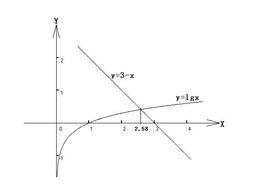
解法
這類方程除極少數情形(如簡單的三角方程)外,只能近似地數值求解,此種數值解法的研究至今仍是計算數學的主要課題。超越方程的數值解法也適用於代數方程。
求解超越方程的近似解法有很多,圖象法雖然形象,但得到的解誤差太大了。常用的近似解法有牛頓切線法、冪級數解法等等,現在也可以編制一段程式用計算機求解,或者利用現成的軟體求解,例如大多數電腦都安裝的EXCEL也可以用來求解超越方程。
matlab軟體是獲得數值解的一個最強大的工具。常用的命令有fsolve, fzero 等,但超越方程的解很難有精確的表達式,因此在matlab中常用eval()函式得到近似數值解,再用vpa()函式控制精度。
 超越方程
超越方程二分法,如右圖
 超越方程
超越方程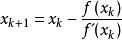 超越方程
超越方程疊代法:解超越方程的主要方法,既適用於求實根,也適用於求復根。使用這類方法時一般需要知道根的足夠好的近似值。最常用的方法有牛頓法、割線法、二次插值法、雙曲插值法、切比雪夫疊代法、艾特肯δ2加速方法和斯梯芬森方法等。
牛頓法:也稱切線法,其計算公式為z0為事先選定的根的初始近似。設z為 ƒ(z)的根,若ƒ(z)在z的某鄰域內二次可微,且ƒ┡(z)≠0,則當z0與z充分接近時,牛頓法至少是二階收斂的,即當k充分大時有估計式成立,C為確定的常數。一般說來,牛頓法只具有局部收斂性,即僅當初始近似與根充分接近時才收斂。但是,當ƒ(x)為實函式,且於[α,b]上ƒ┡(x)和 ƒ″(x)不變號時,若ƒ(x)於[α,b]上有根,則只要初始近似x0滿足條件ƒ(x0) ƒ″(x0)>0,牛頓法就收斂。一般情形,為減弱對初始近似的限制,可利用牛頓下降算法,其算式為ωk>0為疊代參數,由條件│ƒ(z)│z)│確定,牛頓法的k+1次近似z是ƒ(z)在z處的泰勒展開式的線性部分的根。
割線法:又稱弦位法,其算式為z0、z1為初始近似。若ƒ(z)於其根z的某鄰域二次連續可微,且ƒ┡(z)≠0,則z、z與z充分接近時,割線法收斂於z,並當k充分大時有估計式式中C為常數,割線法的k+1次近似z是以z、z為插值節點的線性插值函式的根,如果利用更精確的近似表達式則可構造出更高階的疊代法。
二次插值法:亦稱繆勒方法,是利用二次插值多項式構造的疊代算法。設已確定了z、z、z則z就取為以z、z、z為節點的二次插值多項式兩個根中與zk最接近者,其算式為式中“±”號選成使分母的模為最大者,而
式中當分母為0,則λk=1。
雙曲插值法 :利用線性分式插值構造的疊代算法,其算式為式中μ、δ、Δz和ƒ的意義與二次插值法相同。
若ƒ(z)在其根z的某鄰域內三次可微,並且z0、z1、z2與z充分接近,則二次插值法和雙曲插值法均收斂。此外,如果ƒ┡(z)≠0,對充分大的k,有估計式式中C為確定常數,τ為方程式t3-t2-t-1=0的惟一正根,τ=1.839…。
切比雪夫疊代法:三階收斂的方法,其算式為當ƒ(z)在其根z的鄰域內三次可微且ƒ┡(z)≠0時,對充分大的k,有C為確定常數。
艾特肯δ2加速方法 :提高疊代法收斂速度的有效算法,設{z}為疊代序列,δ2加速的算式為若ƒ(z)在其根z處充分光滑,且ƒ(z)≠0,則對充分大的k,有並且若z是p(p>1)階收斂,即C0均為常數。當ƒ┡(z)=0時也有加速作用。此算法可以循環使用。
斯梯芬森方法:不算微商而二階收斂的方法,其算式為它可由疊代算法循環使用 δ2程式導出。
所有的疊代法用於求重根(即ƒ┡(z)=0)時, 其收斂速度將變慢,收斂階將降低。
為求得達到所需精度的解而花費的代價是評價疊代法優劣的依據,效能指數是其重要指標,它定義為p1/寶,p為收斂階,μ為每步需要計算的函式值和微商值的總數。效能指數越大,說明方法越好。二分法及上述各種疊代法的收斂階(單根時和重根時)和效能指數如表。
只有當初始近似與解充分接近時,疊代法才收斂,這是所述算法的共同特點。減弱對初始近似的限制是提高疊代法有效性的重要措施,例如,牛頓法中引進下降因子。對一些特殊函式類(如單調函式,只有實根的解析函式等)的大範圍收斂疊代算法也有一些研究工作。
舉例
以下的方程分別因為有指數函式、三角函式等超越函式,因此均為超越方程。
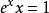 超越方程
超越方程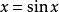 超越方程
超越方程在天文學中,有關軌道偏近點角E的克卜勒方程也是超越方程:
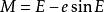 超越方程
超越方程其中:
M為軌道的平近點角。
e為軌道的離心率。