基本介紹
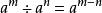 負指數冪
負指數冪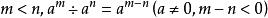 負指數冪
負指數冪在指數法則 中,如果 ,則就產生了 負指數冪。
定義負指數冪等於把冪指數變號後所得的冪的倒數。也就是
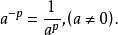 負指數冪
負指數冪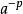 負指數冪
負指數冪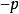 負指數冪
負指數冪 負指數冪
負指數冪應該知道,負指數冪也是不能用正整指數冪的意義來解釋的。也就是說“ ”不能認為是“ 個 相乘”的意思。另外在定義中規定底數不得為零,其原因是和零指數冪的定義是一樣的。
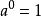 負指數冪
負指數冪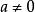 負指數冪
負指數冪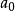 負指數冪
負指數冪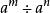 負指數冪
負指數冪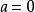 負指數冪
負指數冪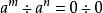 負指數冪
負指數冪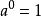 負指數冪
負指數冪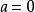 負指數冪
負指數冪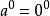 負指數冪
負指數冪在 中規定, ,這是因為 產生於 , 當 時, ,我們知道0是不能作除數的, 所以 中,當 時, 這是沒有意義的 。
相關概念
冪
 負指數冪
負指數冪 負指數冪
負指數冪 負指數冪
負指數冪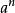 負指數冪
負指數冪 負指數冪
負指數冪n個 相乘的積稱為“ 的n次冪”或“ 的n次乘方”記作 , 是底數,n是指數。這裡n可以是分數、負數,分別稱為“分指數冪”、“負指數冪”,也可以是任意實數或複數。
分指數冪
 負指數冪
負指數冪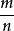 負指數冪
負指數冪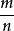 負指數冪
負指數冪 負指數冪
負指數冪當冪的指數為分數時,稱為“分指數冪”。正數 的 次冪( 是既約正分數)定義為 的m次冪的n次算術根,就是:
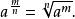 負指數冪
負指數冪乘方
 負指數冪
負指數冪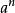 負指數冪
負指數冪 負指數冪
負指數冪(1)n個 相乘的積 稱為 的n次“乘方”,參見“冪”。
 負指數冪
負指數冪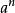 負指數冪
負指數冪(2)從 求 的運算,稱為“乘方”。
正整數指數冪
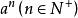 負指數冪
負指數冪 負指數冪
負指數冪 負指數冪
負指數冪 負指數冪
負指數冪 負指數冪
負指數冪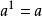 負指數冪
負指數冪 負指數冪
負指數冪一般地, 叫作 的 次冪, 叫作冪的 底數, 叫作冪的 指數,並且規定 。我們注意到在 的n次冪定義中,n是正整數,因此通常又把它稱為 正整數指數冪 。
容易驗證,正整數指數冪的運算滿足如下法則:
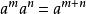 負指數冪
負指數冪(1) ;
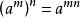 負指數冪
負指數冪(2) ;
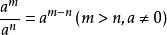 負指數冪
負指數冪(3) ;
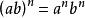 負指數冪
負指數冪(4) 。
負整數指數冪
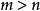 負指數冪
負指數冪在法則(3)中規定了 ,如果取消這個限制,就需要討論下面兩種情形:
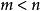 負指數冪
負指數冪❶當 時,冪的商有如下運算:
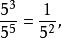 負指數冪
負指數冪依照法則(3)則有
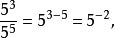 負指數冪
負指數冪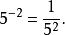 負指數冪
負指數冪即
這就說明當指數為負整數時,冪的值是有意義的。此時規定
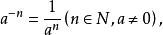 負指數冪
負指數冪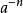 負指數冪
負指數冪叫作 負整數指數冪。
零指數冪
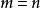 負指數冪
負指數冪❷當 時,冪的商有如下運算:
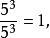 負指數冪
負指數冪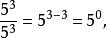 負指數冪
負指數冪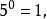 負指數冪
負指數冪且 故
這說明當指數為零時,冪的值是有意義的。此時規定
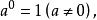 負指數冪
負指數冪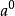 負指數冪
負指數冪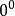 負指數冪
負指數冪叫作 零指數冪,又叫零次冪。但是 是無意義的。
正整數指數冪、負整數指數冪、零指數冪統稱為整數指數冪。正整數指數冪的運算法則對整數指數冪仍然是成立的。特別地,有
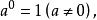 負指數冪
負指數冪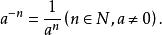 負指數冪
負指數冪整數指數冪的運算法則
同上所述,容易驗證,正整數指數冪的運算滿足如下法則:
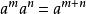 負指數冪
負指數冪(1) ;
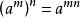 負指數冪
負指數冪(2) ;
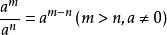 負指數冪
負指數冪(3) ;
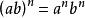 負指數冪
負指數冪(4) 。
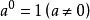 負指數冪
負指數冪(5) ;
註:①這些運算性質在整數指數範圍內仍然適用。
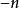 負指數冪
負指數冪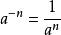 負指數冪
負指數冪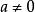 負指數冪
負指數冪 負指數冪
負指數冪②任何不等於零的數的 (n為正整數)次冪,等於這個數的n次冪的倒數,即 ( ,n為正整數)。在這兩個冪的意義中,強調底數 都不等於零,否則無意義。
③學習了零指數冪和負整數指數冪後,正整數指數冪的運算性質可以推廣到整數指數幕的範圍 。
冪的運算法則
當指數概念擴充到任意實數之後,冪的運算法則可合併為 :
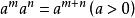 負指數冪
負指數冪(1) ;
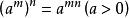 負指數冪
負指數冪(2) ;
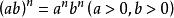 負指數冪
負指數冪(3) 。