指數冪

一般地，在數學上我們把n個相同的因數a相乘的積記做a^n。這種求幾個相同因數的積的運算叫做乘方，乘方的結果叫做冪。在a^n中,a叫做底數,n叫做指數。a^n讀作“a的n次方”或“a的n次冪“。 一個數可以看做這個數本身的一次方。例如，5就是5^1，指數1通常省略不寫。二次方也叫做平方，如5^2通常讀做”5的平方“；三次方也叫做立方，如5^3可讀做”5的立方“。

基本信息

• 中文名稱：指數冪
• 外文名：Exponent
• 別稱：多個相同因數乘方後的結果
• 創始人：徐光啟
• 學科門類：高等數學
• 學科分類：高等數學
• 研究對象：精確計算領域
• 代表人物：徐光啟
• 學科套用：高等數學

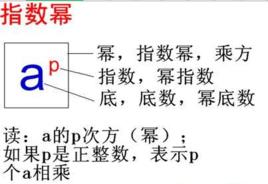
指數冪的運算法則

乘法

1. 同底數冪相乘，底數不變，指數相加。

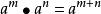指數冪

即 (m,n都是 有理數)。

2. 冪的乘方，底數不變，指數相乘。

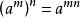指數冪

即 (m,n都是 有理數)。

3. 積的乘方，等於把積的每一個因式分別乘方，再把所得的冪相乘。

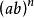指數冪

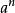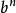指數冪

指數冪

即= · (m,n都是 有理數)。

4.分式乘方, 分子分母各自乘方。

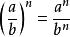指數冪

即(b≠0)。

除法

1. 同底數冪相除，底數不變，指數相減。

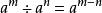指數冪

即( a≠0，m,n都是 有理數 )。

2. 規定：

(1) 任何不等於零的數的零次冪都等於1。

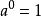指數冪

即( a≠0)。

(2)任何不等於零的數的-p（p是 正整數）次冪，等於這個數的p次冪的倒數。

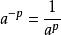指數冪

即( a≠0,p是 正整數)。

（規定了零指數冪與負整數指數冪的意義，就把指數的概念從正整數推廣到了整數。正整數指數冪的各種運算法則對整數指數冪都適用。）

混合運算

對於乘除和乘方的混合運算，應先算 乘方，後算 乘除；如果遇到括弧，就先進行 括弧 里的運算。

注意

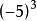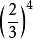指數冪

指數冪

冪的底數是 分數 或負數時，底數應該 添上 括弧，如，。