簡單介紹
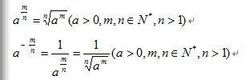 分數指數冪
分數指數冪分數指數冪是根式的另一種表示形式,
即n次根號(a的m次冪)可以寫成a的m/n次冪。
冪是指數值,如8的1/3次冪=2
一個數的b分之a次方等於b次根號下這個數的a次方
重點:
1、分數指數冪的含義的理解。
2、根式與分數指數冪的互化。
3、有理指數冪的運算性質。
難點:
1、分數指數冪概念的理解。
2、有理指數冪的運算和化簡
證明
a^(m/n)=(a^m)開n次方,(a>0,m、n∈Z且n>1)
證:
令(a^m)開n次方=b
兩邊取n次方,有
a^m=b^n
a^(m/n)=(a^m)^(1/n)=(b^n)^(1/n)=b=(a^m)開n次方
即a^(m/n)=(a^m)開n次方
意義
規定:正數的正分數指數冪的意義是——a的n分之m次方=n√a的m次方(a>0,m、n屬於正整數,n>1)
0的正分數指數冪等於0,0的負分數指數冪沒有意義
指出:規定了分數指數冪的意義後,指數的概念就從整數指數推廣到了有理數指數,那么整數指數冪的運算性質也同樣可以推廣到有理數指數冪.
運算性質:
對於任意有理數r,s,均有下面的運算性質
(1)a^r×a^s=a^(r+s)(a>0,r,s∈Q)
(2)(a^r)^s=a^rs(a>0,r,s∈Q)
(3)(ab)^r=a^r×b^r(a>0,b>0,r∈Q)
根式與分數指數冪的互化:
這部分經常弄錯。根號左上角的數當分數指數冪的分母,根號裡面各個因式或因數的指數當分數指數冪的分子,注意,各個因式(因數)如果指數不同,要分開寫。即是內做子,外做母,同母可不同子。
有理指數冪的運算和化簡:
第一步是找同底數冪,調換位置時注意做到不重不漏,接著就是合併同類項,同底數冪的相乘,底數不變,指數相加,相除的話就是底數不變,指數相減。同底數冪相加減,能化簡的合併化簡,不能的按照降冪或升冪排列。
用電腦利用分數指數冪進行多次根號計算:
在查看中,改為“科學型”。先輸入底數,再按“y^x”,接下來如果是3次根號邊輸入“3”“1/x”,以此類推。最後按等於得出結果。實例:27的三次根號,“27”“y^x”“3”“1/x”“=”得出結果3.