摘要
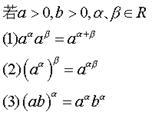 冪的運算
冪的運算冪的運算
一、教學內容:
1.同底數冪的乘法
2.冪的乘方與積的乘方
3.同底數冪的除法
二、技能要求:
掌握正整數冪的運算性質(同底數冪的乘法、冪的乘方、積的乘方、同底數冪的除法),能用字母式子和文字語言正確地表述這些性質,並能運用它們熟練地進行運算。
三、主要數學能力
1.通過冪的運算到多項式乘法的學習,初步理解“特殊——一般——特殊”的認識規律,發展思維能力。
2.在學習冪的運算性質、乘法法則的過程中,培養觀察、綜合、類比、歸納、抽象、概括等思維能力。
四、學習指導
1.同底數冪的乘法:am·an=am+n (m, n是自然數)
同底數冪的乘法法則是本章中的第一個冪的運算法則,也是整式乘法的主要依據之一。學習這個法則時應注意以下五個問題:
(1)先弄清楚底數、指數、冪這三個基本概念的涵義。
(2)它的前提是“同底”,而且底可以是一個具體的數或字母,也可以是一個單項式或多項式,如:
(2x+y)2·(2x+y)3=(2x+y)5,底數就是一個二項式(2x+y)。
(3)指數都是正整數
(4)這個法則可以推廣到三個或三個以上的同底數冪相乘,即am·an·ap....=am+n+p+... (m, n, p都是自然數)。
(5)不要與整式加法相混淆。乘法是只要求底數相同則可用法則計算,即底數不變指數相加,如:
x5·x4=x5+4=x9;而加法法則要求兩個相同;底數相同且指數也必須相同,實際上是冪相同係數相加,
如-2x5+x5=(-2+1)x5=-x5,而x5+x4就不能合併。
例1.計算:(1) (- )(- )2(- )3 (2) -a4·(-a)3·(-a)5
解:(1) (- )(- )2(- )3 分析:①(- )就是(- )1,指數為1
=(- )1+2+3 ②底數為- ,不變。
=(- )6 ③指數相加1+2+3=6
= ④乘方時先定符號“+”,再計算 的6次冪
解:(2) -a4·(-a)3·(-a)5 分析:①-a4與(-a)3不是同底數冪
=-(-a)4·(-a)3·(-a)5 可利用-(-a)4=-a4變為同底數冪
=-(-a)4+3+5 ②本題也可作如下處理:
=-(-a)12 -a4·(-a)3·(-a)5=-a4(-a3)(-a5)
=-a12 =-(a4·a3·a5)=-a12
例2.計算(1) (x-y)3(y-x)(y-x)6
解:(x-y)3(y-x)(y-x)6 分析:(x-y)3與(y-x)不是同底數冪
=-(x-y)3(x-y)(x-y)6 可利用y-x=-(x-y), (y-x)6=(x-y)6
=-(x-y)3+1+6 變為(x-y)為底的同底數冪,再進行
=-(x-y)10 計算。
例3.計算:x5·xn-3·x4-3x2·xn·x4
解:x5·xn-3·x4-3x2·xn·x4 分析:①先做乘法再做減法
=x5+n-3+4-3x2+n+4 ②運算結果指數能合併的要合併
=x6+n-3x6+n ③3x2即為3·(x2)
=(1-3)x6+n ④x6+n,與-3x6+n是同類項,
=-2x6+n 合併時將係數進行運算(1-3)=-2
底數和指數不變。
2.冪的乘方(am)n=amn,與積的乘方(ab)n=anbn
(1)冪的乘方,(am)n=amn,(m, n都為正整數)運用法則時注意以下以幾點:
①冪的底數a可以是具體的數也可以是多項式。如[(x+y)2]3的底數為(x+y),是一個多項式,
[(x+y)2]3=(x+y)6
②要和同底數冪的乘法法則相區別,不要出現下面的錯誤。如:
(a3)4=a7; [(-a)3]4=(-a)7; a3·a4=a12
(2)積的乘方(ab)n=anbn,(n為正整數)運用法則時注意以下幾點:
①注意與前二個法則的區別:積的乘方等於將積的每個因式分別乘方(即轉化成若干個冪的乘方),再把所得的冪相乘。
②積的乘方可推廣到3個以上因式的積的乘方,如:(-3a2b)3
如(a1·a2·…….an)m=a1m·a2m·…….ANM
例4.計算:①(a2m)n ②(am+n)m ③(-x2yz3)3 ④-(ab)8
解:①(a2m)n 分析:①先確定是冪的乘方運算
=a(2m)n ②用法則底數a 不變指數2m和n相乘
=a2mn
②(am+n)m 分析:①底數a不變,指數(m+n)與m相乘
=a(m+n)m
= ②運用乘法分配律進行指數運算。
③(-x2yz3)3 分析:①底數有四個因式:(-1), x2, y, z3
=(-1)3(x2)3y3(z3)3 分別3次方
=-x6y3z9 ②注意(-1)3=-1, (x2)3=x2×3=x6
④-(ab)8 分析:①8次冪的底數是ab。
=-(a8b8) ②“-”在括弧的外邊先計算(ab)8
=-a8b8 再在結果前面加上“-”號。
例5.當ab= ,m=5, n=3, 求(ambm)n的值。
解:∵ (ambm)n 分析:①對(ab)n=anbn會從右向左進行逆
=[(ab)m]n 運算 ambm=(ab)m
=(ab)mn ②將原式的底數轉化為ab,才可將ab
∴ 當m=5, n=3時, 代換成 。
∴ 原式=( )5×3 ( )15應將 括起來不能寫成 15。
=( )15
例6.若a3b2=15,求-5a6b4的值。
解:-5a6b4 分析:a6b4=(a3b2)2
=-5(a3b2)2 套用(ab)n anbn
=-5(15)2
=-1125
例7.如果3m+2n=6,求8m·4n的值。
解:8m·4n 分析:①8m=(23)m=23m
=(23)m·(22)n 4n=(22)n=22n
=23m·22n ②式子中出現3m+2n可用6
=23m+2n 來代換
=26=64
3. 同底數冪的除法:
(1)同底數冪的除法:am÷an=am-n (a≠0, m, n均為正整數,並且m>n)
①同底數冪的除法是整式除法的基礎,要熟練掌握。同底數冪的除法法則是根據除法是乘法的逆運算歸納總結出來的,和前面講的冪的運算的三個法則相比,在這裡底數a是不能為零的,否則除數為零,除法就沒有意義了。又因為在這裡沒有引入負指數和零指數,所以又規定m>n。能從特殊到一般地歸納出同底數冪的除法法則。
②同底數冪的兩個冪相除,如果被除式的指數與除式的指數相等,那么商等於1,即am÷am=1,m是任意自然數。a≠0, 即轉化成a0=1(a≠0)。
③同底數冪的兩個冪相除,如果被除式的指數小於除式的指數,即m-n<0時,指數部分為負整數則轉化成負整數指數冪,再用負整數指數冪法則。
④要注意和其它幾個冪的運算法則相區別。
⑤還應強調:am·an=am+n與am+n÷an=am的互逆運算關係,同時指數的變化也是互逆運算關係,應溝通兩者的聯繫。
(2)零指數:a0=1 (a≠0)
①條件是a≠0,00無意義。
②它是由am÷an=am-n當a≠0,m=n時轉化而來的。也就是說當同底數冪相除時,被除式指數與除式的指數相等時即轉化成零指數冪,它的結果為1。
(3)負整數指數冪:a-p= (a≠0, p是正整數)
①當a=0時沒有意義,0-2, 0-3都無意義。
②它是由am÷an=am-n 當a≠0, m<n時轉化而來的。也就是說當同底數冪相除時,被除式指數小於除式指數時即轉化成負指數冪。a-p結果為ap的倒數,也就是說一個不為零的數的負整數指數冪等於這個數正整數指數冪的倒數,也可以等於這個數倒數的正整數指數冪,即a-p=( )p (a≠0,p為自然數)
