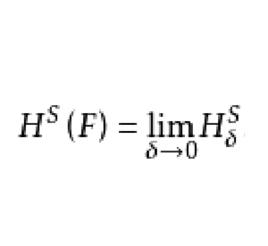基本介紹
 豪斯多夫測度
豪斯多夫測度 豪斯多夫測度
豪斯多夫測度設在n維歐氏空間中對子集定義其直徑為
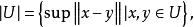 豪斯多夫測度
豪斯多夫測度 豪斯多夫測度
豪斯多夫測度 豪斯多夫測度
豪斯多夫測度如果子集族為可數個直徑不超過的集構成的覆蓋F的集類,即
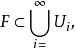 豪斯多夫測度
豪斯多夫測度 豪斯多夫測度
豪斯多夫測度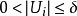 豪斯多夫測度
豪斯多夫測度 豪斯多夫測度
豪斯多夫測度 豪斯多夫測度
豪斯多夫測度 豪斯多夫測度
豪斯多夫測度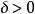 豪斯多夫測度
豪斯多夫測度且對每一個都有,則稱是F的一個覆蓋。設F是中的任一子集,S為一非負數,對任意,定義
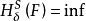 豪斯多夫測度
豪斯多夫測度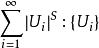 豪斯多夫測度
豪斯多夫測度 豪斯多夫測度
豪斯多夫測度 豪斯多夫測度
豪斯多夫測度{為的覆蓋} (1)
 豪斯多夫測度
豪斯多夫測度 豪斯多夫測度
豪斯多夫測度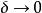 豪斯多夫測度
豪斯多夫測度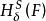 豪斯多夫測度
豪斯多夫測度考察所有直徑不超過的的覆蓋,並讓這些直徑的S次冪的和達到最小。當時,趨於一極限值,可寫為
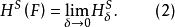 豪斯多夫測度
豪斯多夫測度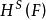 豪斯多夫測度
豪斯多夫測度 豪斯多夫測度
豪斯多夫測度 豪斯多夫測度
豪斯多夫測度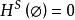 豪斯多夫測度
豪斯多夫測度 豪斯多夫測度
豪斯多夫測度 豪斯多夫測度
豪斯多夫測度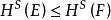 豪斯多夫測度
豪斯多夫測度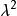 豪斯多夫測度
豪斯多夫測度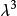 豪斯多夫測度
豪斯多夫測度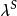 豪斯多夫測度
豪斯多夫測度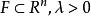 豪斯多夫測度
豪斯多夫測度稱為的維豪斯多夫測度。通常測度只是賦予集以數值“大小”的一種方式,如果集是以合理的方式分解為有限或可數個部分,則整體的數值應該是所有部分數值之和。可以證明,對於空集∅,有。如果包含於內,則。豪斯多夫測度具有平移不變性與旋轉不變性。長度、面積和體積具有眾所周知的比例性質,即當比例放大λ倍時,曲線的長度放大λ倍,平面區域的面積則放大倍,而三維物體的體積則放大倍。由此可預料,S維豪斯多夫測度的放大倍數為。其數學表達式為:若,則
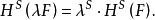 豪斯多夫測度
豪斯多夫測度其他介紹
 豪斯多夫測度
豪斯多夫測度 豪斯多夫測度
豪斯多夫測度豪斯多夫測度(Hausdorff measure)是幾何測度論中一類有重要意義的測度。在歐氏空間情形,對任意和給定的,令
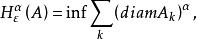 豪斯多夫測度
豪斯多夫測度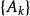 豪斯多夫測度
豪斯多夫測度這裡使得
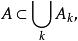 豪斯多夫測度
豪斯多夫測度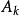 豪斯多夫測度
豪斯多夫測度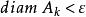 豪斯多夫測度
豪斯多夫測度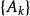 豪斯多夫測度
豪斯多夫測度且每個的直徑(ε是任意給定正數),下確界對所有這樣的而取。定義
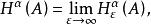 豪斯多夫測度
豪斯多夫測度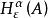 豪斯多夫測度
豪斯多夫測度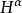 豪斯多夫測度
豪斯多夫測度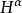 豪斯多夫測度
豪斯多夫測度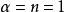 豪斯多夫測度
豪斯多夫測度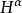 豪斯多夫測度
豪斯多夫測度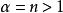 豪斯多夫測度
豪斯多夫測度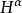 豪斯多夫測度
豪斯多夫測度 豪斯多夫測度
豪斯多夫測度 豪斯多夫測度
豪斯多夫測度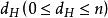 豪斯多夫測度
豪斯多夫測度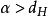 豪斯多夫測度
豪斯多夫測度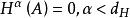 豪斯多夫測度
豪斯多夫測度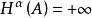 豪斯多夫測度
豪斯多夫測度 豪斯多夫測度
豪斯多夫測度 豪斯多夫測度
豪斯多夫測度 豪斯多夫測度
豪斯多夫測度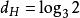 豪斯多夫測度
豪斯多夫測度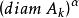 豪斯多夫測度
豪斯多夫測度(是隨ε減小而增大的,故此定義有意義),則是度量外測度,稱為 豪斯多夫外測度。由這個外測度所確定的(惟一的)測度即為豪斯多夫測度,仍用表示。豪斯多夫測度是正則波萊爾測度,當時,就是直線上的勒貝格測度;時,與上的勒貝格測度等價,但不完全相同。豪斯多夫測度的意義在於,對的任一子集A,存在數,使時時,因而刻畫了中集合的“維數”(參見“豪斯多夫維數”)。但一般不是整數,例如對於直線上的康托爾集,。這個測度由豪斯多夫(F.Hausdorff)於1918年引進,在調和分析、位勢論等學科中有套用。豪斯多夫測度還可在一般的度量空間上和更廣的意義(將上述定義中的()換成某個集函式之值)下定義 。