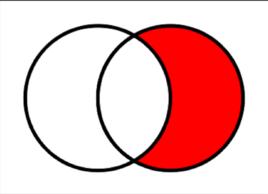
簡介
根據ISO 31-11標準,B中A的相對補集表示為B∖A。 它有時被寫為B-A,但是這個符號是不明確的,因為在某些情況下,它可以被解釋為所有元素b-a的集合,其中b取自B,而A來自A。
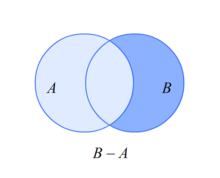 相對補集
相對補集如果A和B是集合,則在B中的A的相對補集也稱為B和A的集合差,其元素屬於 B,但不屬於 A。 A在 B中的相對補集通常寫作 B - A,讀作“ A在 B中的相對補集”。
形式上:
B \ A=B - A = { x | x∈B,x ∉ A}。
例如:
{1,2,3} - {2,3,4}={1}.
{2,3,4} - {1,2,3}={4}.
若 R是實數集合 Q 是有理數集合,則 R - Q 為無理數集合。
另外,補集存在 相對補集與 絕對補集。
A在B中的相對補集其實就是 A∩B在B中的絕對補集。
性質
A,B,C是三個集合。 以下是相對補集的屬性:
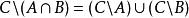 相對補集
相對補集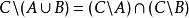 相對補集
相對補集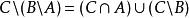 相對補集
相對補集特殊情況
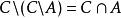 相對補集
相對補集表明該交集可以僅可以使用相對補集來表示。
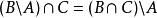 相對補集
相對補集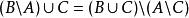 相對補集
相對補集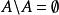 相對補集
相對補集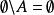 相對補集
相對補集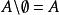 相對補集
相對補集絕對補集
定義
如果A是集合,則A的絕對補集(或簡稱A的補集)是不在A中的元素集合。換句話說,如果U是包含正在所有元素的宇宙,那么A的絕對補集是U中A的相對補集 :
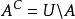 相對補集
相對補集形式上:
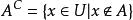 相對補集
相對補集A的絕對補集通常由A 表示。
舉例
假設全集是整數集。 A是奇數集,則A的絕對補集是偶數集。
假設全集是一副標準的54張撲克牌。集合A是大小王,那么A的絕對補集就是其餘52張牌。
性質
讓A和B在全集中成為兩組。以下絕對補集的重要屬性:
德摩根定律:
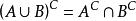 相對補集
相對補集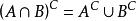 相對補集
相對補集補充法:
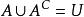 相對補集
相對補集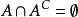 相對補集
相對補集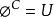 相對補集
相對補集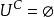 相對補集
相對補集這取決於條件與其對立的等價性。
卷積或雙重補充法:
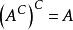 相對補集
相對補集相對補集和絕對補集之間的關係:
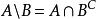 相對補集
相對補集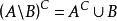 相對補集
相對補集與設定差的關係:
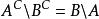 相對補集
相對補集上面的前兩項補充法則表明,如果A是U的非空子集,則{A,A }是U分開的兩個集。