主要特點
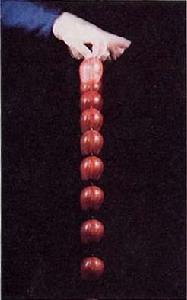 自由落體
自由落體自由落體運動的特點,體現在“自由”二字上,其含意為:物體開始下落時是靜止的即v0=0。如果給物體一個初速度豎直下落,不能算自由落體。物體在下落過程中,除受重力作用外,不再受其他任何作用力(包括空氣阻力)。
計算公式
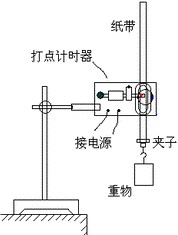 研究自由落體的打點計時器
研究自由落體的打點計時器通常在空氣中,隨著自由落體運動速度的增加,空氣對落體的阻力也逐漸增加。當物體受到的重力等於它所受到的阻力時,落體將勻速降落,此時它所達到的最高速度稱為終端速度。例如傘兵從飛機上跳下時,若不張傘其終端速度約為50米/秒,張傘時的終端速度約為6米/秒。
關係自由落體各物理量的關係:如果下落時間為t,瞬時速度為vt,位移為X,g為重力加速度,則有以下關係:(見右圖)
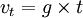 自由落體
自由落體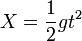 自由落體
自由落體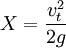 自由落體
自由落體相關定律
物理量關係
基於(物體位於近地面附近)重力是個常數的假設下,根據萬有引力定律,此時萬有引力充當向心力,即有重力是與物體的質量成正比G=mg。重力加速度以g表示一個常數。它是矢量,平均值為9.81,
單位是m/s²(米每二次方秒),SI單位是N/kg。這個加速度是由於物體受到了地球的萬有引力產生的。假定除了重力外不受其它力的作用,物體在下落中的路程的長度與經過的時間平方成正比。
在下落的過程中,物體無論在哪個高度也不論是否具有速度,都具有重力勢能,其數值同樣也是Ep=mgh。如果物體在下落過程中不受其它力的作用,且可以忽略空氣阻力時,其總能量遵守機械能守恆定則,即重力勢能和動能的總和守恆。我們常常用機械能守恆定則來計算,物體可能達到的最大高度,和落到地面瞬間的最大速度。
注意,在實際計算和套用問題中,應考慮g值隨緯度和高度變化的問題,但在一般的高中問題中,經常給出g值為10米每二次方秒,僅為計算簡單而考慮,不可自行“舉一反三”地套用到其它問題中。
如果下落時間為t,瞬時速度為vt,位移為X,g為重力加速度,則有以下關係:
規律
通常在空氣中,隨著自由落體的運動速度的增加,空氣對落體的阻力也逐漸增加。
當物體受到的重力等於它所受到的阻力時,落體將勻速降落,此時它所達到的最高速度稱為終端速度。例如傘兵從飛機上跳下時,若不張傘其終端速度約為50米/秒,張傘時的終端速度約為6米/秒。
g是重力加速度,g≈9.8m/(s^2);
(1)速度隨時間變化的規律:v=gt。
(2)位移隨時間變化的規律:h=(1/2)gt^2。
(3)速度隨位移的變化規律:2gs=v^2。
推論
(1)相鄰相等時間T內的位移之差△h=gT^2(2)一段時間內平均速度v=h/t=1/2gt
概念
自由落體的“落體”,顧名思義是指物體在只受重力作用下,由高空自由下落,關鍵是“自由”二字,其含意為:其一,物體開始下落時是靜止的,即初速度為0,如果給物體一個初速度豎直下落,不能算自由落體,只能算是加速度不變的勻加速運動,其二,物體在下落過程中,除受重力作用外,不再受其他任何作用力(如空氣阻力)。
勻加速直線運動,其加速度恆等於重力加速度g(g=9.8m/(s^2))。
定律
據伽利略“自由落體”定律,物體下落的加速度與物體的重量無關,也與物體的質量無關,就人們所談比薩斜塔的落體實驗而言,大鉛球與小鉛球都會同時落地,同時擊響地面的木板。而按牛頓的“萬有引力”定律計算,大鉛球(m大)與地球M之間的引力(F大)應大於小鉛球(m小)與地球M之間的引力(F小),故大鉛球應該先落地,小鉛球隨後落地,伽利略自由落體實驗的結果顯然不能體現這種引力差異。即:
(F大=G·m大M/r的2次方)>(F小=G·m小M/r的2次方)
就同一個鉛球m在同一高度h而言,如果在地球上落下的時間需要1秒,那么在月球上落入月面的時間就會大於1秒,這又能有效地體現牛頓“萬有引力”定律中的質量因素。即地球質量大於月球質量,故在吸引同一物體時,地球上的重力加速度g就會大於月球上的加速度g′。即:
(g地=GM地/h的2次方)>(g′月=GM月/h的2次方)
歷史由來
亞里士多德
 亞里士多德
亞里士多德亞里士多德(前384—前322年),古希臘斯吉塔拉人,世界古代史上最偉大的哲學家、科學家和教育家之一。是柏拉圖的學生,亞歷山大的老師。公元前335年,他在雅典辦了一所叫呂克昂的學校,被稱為逍遙學派。馬克思曾稱亞里士多德是古希臘哲學家中最博學的人物,恩格斯稱他是古代的黑格爾。
伽利略
 比薩斜塔
比薩斜塔伽利略是義大利天文學家,也是世界著名物理學家。他於1564年誕生在義大利北部的比薩市,1642年1月8日去世,終年78歲。他畢生致力於科學事業,不僅為我們留下了時鐘、望遠鏡和眾多的科學專著,而且還為破除宗教迷信、科學偏見作出了傑出的貢獻。
伽利略在比薩大學讀書時,對校方經常向學生灌輸上帝創造萬物之類的宗教信條非常反感,他只是潛心於自己在科學理論上的新發現。有一次,神父在比薩教堂給學生們講聖經,伽利略卻盯住教堂屋頂上搖晃的銅吊燈觀察著,他發現,吊燈左右搖擺的來回時間始終是一樣的。由此,他發現了“擺錘的等時性”,並在工匠的配合下,製成了有史以來第一台擺錘時鐘。後來他又製成了世界上第一台天平儀,還為此寫了一篇題為《固體內的重心》的論文,這使21歲的伽利略引起了全義大利學者的普遍重視。1589年,年輕的伽利略又在著名的比薩斜塔上做了轟動一時的自由落體實驗。伽利略把兩個不同重量的鐵球從斜塔上扔下來,結果兩個鐵球同時落地,從而推翻了古希臘學者亞里士多德在一千多年前宣布的“不同重量物體落地速度不同”的理論。
伽利略在哥白尼·布魯諾的“日心說”鼓舞下,開始向教皇奉為至寶的“地心說”發起挑戰,他要徹底戳穿“地球是中心,上帝是主宰”的騙人謊話。為了便於戰鬥,他製造了第一架天文望遠鏡。由於視野的延伸,他看到了月亮上的山谷、太陽上的黑子,甚至還發現了木星的四顆衛星——即著名的伽利略衛星。
伽利略在科學領域裡的重大成就,激怒了羅馬教皇及其信徒們,當伽利略寫了《關於兩種世界體系對話》這篇科學巨著後,教會終於露出了猙獰面目,把伽利略投入了監獄。教皇烏爾班八世的御用工具宗教裁判所在1633年6月21日宣布對伽利略的判決說:“我們判決你在宗教法庭監獄內服刑,刑期由我們掌握,為了有益於補贖,命令你在今後3年內,每周背誦7篇贖罪詩篇……”這一紙胡言,竟使伽利略蒙冤300多年,至死都沒有撤銷判決,甚至死後還被禁止舉行殯禮,不準葬入聖太克羅斯墓地。
但真理是不可抗拒的。1989年,羅馬教皇承認伽利略是被“錯誤地定了罪”,後來教皇又在世界主教會議上提出重新審理這一案件,為伽利略平反昭雪,綿延達347年的世界科學界大冤案終於得到了公正的裁決。
相關研究
 自由落體
自由落體但是這種從表面上的觀察得出的結論實際上是錯誤的。偉大的物理學家伽利略用簡.單明了的科學推理,巧妙地揭示了亞里士多德的理論內部包含的矛盾。他在1638年寫的《兩種新科學的對話》一書中指出:根據亞里士多德的論斷,一塊大石頭的下落速度要比一塊小石頭的下落速度大。假定大石頭的下落速度為8,小石頭的下落速度為4,當我們把兩塊石頭拴在一起時,下落快的會被下落慢的拖著而減慢,下落慢的會被下落快的拖著而加快,結果整個系統的下落速度應該小於8。但是兩塊石頭拴在一起,加起來比大石頭還要重,因此重物體比輕物體的下落速度要小。這樣,就從重物體比輕物體下落得快的假設,推出了重物體比輕物體下落得慢的結論。亞里士多德的理論陷入了自相矛盾的境地。伽利略由此推斷重物體不會比輕物體下落得快。伽利略曾在著名的比薩斜塔做了著名的自由落體試驗,讓兩個體積相同,質量不同的球從塔頂同時下落,結果兩球同時落地,以實踐駁倒了亞里士多德的結論。(但是後來經過歷史的嚴格考證,伽利略並沒有在比薩斜塔做實驗,人們卻還是把比薩斜塔當作對伽利略的紀念碑)。
提出假說
伽利略認為,自由落體是一種最簡單的變速運動。他構想,最簡單的變速運動的速度應該是均勻變化的。但是,速度的變化怎樣才算均勻呢?他考慮了兩種可能:一種是速度的變化對時間來說是均勻的,即經過相等的時間,速度的變化相等;另一種是速度的變化對位移來說是均勻的,即經過相等的位移,速度的變化相等。伽利略假設第一種方式最簡單,並把這種運動叫做勻變速運動。數學推理
在伽利略的時代,技術不夠發達,通過直接測定瞬時速度來驗證一個物體是否做勻變速運動,是不可能的,但是,伽利略套用數學推理得出結論:做初速度為零的勻變速運動的物體通過的位移與所用時間的平方成正比,即s=at^2;這樣,只要測出做變速運動的物體通過不同位移所用的時間,就可以驗證這個物體是否在做勻變速運動。伽利略是怎樣推出s=gt;的呢?他的思路大致如下:他推斷初速度為零、末速度為v的勻變速運動的平均速度是v/2,然後套用這個關係得出s=vt/2。再套用v=at,就導出s=1/2gt^2。
另:自由落體運動是初速度為零、加速度為g的勻加速直線運動,它是勻變速直線運動的一個特例。因此,勻變速直線運動的基本公式及推論都適用於自由落體運動,只要把公式中的v0取為零,a換成g即可,即:vt=gt,h=1/2gtv=2gh。其中,h為物體由靜止下落的高度。
實驗驗證
自由落體下落的時間太短,當時用實驗直接驗證自由落體是勻加速運動仍有困難,伽利略採用了間接驗證的方法,他讓一個銅球從阻力很小的斜面上滾下,做了上百次的實驗,小球在斜面上運動的加速度要比它豎直下落時的加速度小得多,所以時間容易測量些。實驗結果表明,光滑斜面的傾角保持不變,從不同位置讓小球滾下,小球通過的位移跟所用時間的平方之比是不變的即位移與時間的平方呈正比。由此證明了小球沿光滑斜面向下的運動是勻變速直線運動,換用不同質量的小球重複上述實驗,位移跟所用時間的平方的比值仍不變,這說明不同質量的小球沿同一傾角的斜面所做的勻變速直線運動的情況是相同的。不斷增加大斜面的傾角,重複上述實驗,得出的值隨斜面傾角的增加而增大,這說明小球做勻變速運動的加速度隨斜面傾角的增大而變大。典型例子
關掉火箭的太空航行器月球環繞地球的軌道,地球環繞太陽的軌道,或小行星繞太陽的軌道。地球上,在真空管中下落,例如:物理學展示
NASA的零G研究機構(Zero-GResearchFacility)
與上面自由落體相反地,以下情形是有其他力量同時在作用,包括了:
(1)站在地上,坐在地面上一把椅子上等等(重量被地面的支持力所平衡);
(2)搭乘飛機(重量被機翼提供的升力所平衡);
(3)重返大氣層以及降落傘著陸(重量被反向的空氣阻力所對抗);
(4)太空航行器的軌道動作(此時火箭提供推力)。
合理外推
 自由落體
自由落體伽利略對自由落體的研究,開創了研究自然規律的科學方法,這就是抽象思維、數學推導和科學實驗相結合的方法,這種方法對於後來的科學研究具有重大的啟蒙作用,至今仍不失為重要的科學方法之一。
有可能的話,不妨重複一下伽利略做過的斜面實驗。這裡的關鍵的確是準確測量時間。
幾條推論
1.第1秒末、第2秒末、……、第n秒末的速度之比V1:V2:V3……:Vn=1:2:3:……:n2.從下落開始,物體在每一段相等的時間內通過的位移之比為自然數奇數之比1:3:5:7……2n-1
3.從下落開始,物體在每相鄰兩段相等的時間內通過的位移為at²
4.從下落開始,物體通過1S2S3S4S......ns所用的時間為1:√2:√3:√4:√n
物體通過1s所用的時間為√(2S/g)
物體通過2s所用的時間為√(2S/g)×√2物體通過ns所用的時間為√(2S/g)×√n
且由推論3易得推論4
5.從下落開始,物體通過相等的位移所用的時間為1:√2-1:√3-√2:√4-√3:√n-√(n-1)
各物理量關係
基於(物體位於靠近地球表面)重力是個常數的假設下牛頓的重力定律是F等於m與g的乘積。即重力是與物體的質量成正比F=mg。重力加速度以g表示一個常數。它是矢量,平均值為9.81單位是m/s^2。這個加速度是由於物體受到了重力產生的。物體的最初狀態是靜止的,物體下落中假定除了重力外不受其它力的作用。它下落的路程的長度與經過的時間平方成正比。自由下落物體在下落的最初位置,即最大高度,具備有重力勢能。用下標為P的大寫字母E來表示Ep。它的數值是物體的重力與高度的乘積Ep=mgh。這個表達式只在物體距離地球表面高度很小才有效。在下落的過程中,物體無論在那個高度也不論是否同時具有速度,都具有重力勢能,其數值同樣也是Ep=mgh。
如果下落時間為t,瞬時速度為vt,位移為X,g為重力加速度。
古代的學者們認為,物體下落的快慢是由它們的重量大小決定的,物體越重,下落得越快。生活在公元前4世紀的希臘哲學家亞里士多德最早闡述了這種看法。亞里士多得的論斷影響深遠,在其後兩千多年的時間裡,人們一直信奉他的學說。但是這種從表面上的觀察得出的結論實際上是錯誤的。偉大的物理學家伽利略用簡單明了的科學推理,巧妙地揭示了亞里士多德的理論內部包含的矛盾。他在1638年寫的《兩種新科學的對話》一書中指出:根據亞里士多德的論斷,一塊大石頭的下落速度要比一塊小石頭的下落速度大。假定大石頭的下落速度為8,小石頭的下落速度為4,當我們把兩塊石頭拴在一起時,下落快的會被下落慢的拖著而減慢,下落慢的會被下落快的拖著而加快,結果整個系統的下落速度應該小於8。但是兩塊石頭拴在一起,加起來比大石頭還要重,因此重物體比輕物體的下落速度要小。這樣,就從重物體比輕物體下落得快的假設,推出了重物體比輕物體下落得慢的結論。亞里士多德的理論陷入了自相矛盾的境地。伽利略由此推斷重物體不會比輕物體下落得快。提出假說伽利略認為,自由落體是一種最簡單的變速運動。他構想,最簡單的變速運動的速度應該是均勻變化的。但是,速度的變化怎樣才算均勻呢?他考慮了兩種可能:一種是速度的變化對時間來說是均勻的,即經過相等的時間,速度的變化相等;另一種是速度的變化對位移來說是均勻的,即經過相等的位移,速度的變化相等。伽利略假設第一種方式最簡單,並把這種運動叫做勻變速運動。
數學推理在伽利略的時代,技術不夠發達,通過直接測定瞬時速度來驗證一個物體是否做勻變速運動,是不可能的,但是,伽利略套用數學推理得出結論:做初速度為零的勻變速運動的物體通過的位移與所用時間的方成正比,即s=at^2這樣,只要測出做變速運動的物體通過不同位移所用的時間,就可以驗證這個物體是否在做勻變速運動。伽利略是怎樣推出s=gt^2的呢?他的思路大致如下:先由平均速度得出s=V/t。他推斷初速度為零、末速度為v的勻變速運動的平均速度,然後套用這個關係得出s=vt/2。再套用a=v/t從上式消去v,就導出s=at^2/2,即s=1/2gt^2。
實驗驗證
 因為自由落體而著名的比薩斜塔
因為自由落體而著名的比薩斜塔套用
1、關掉火箭的太空航行器月球環繞地球的軌道,地球環繞太陽的軌道,或小行星繞太陽的軌道。地球上,在真空管中下落,例如:物理學展示NASA的零G研究機構(Zero-GResearchFacility)。與上面自由落體相反地,以下情形是有其他力量同時在作用,包括了:(1)站在地上,坐在地面上一把椅子上等等(重量被地面的支持力所平衡);
(2)搭乘飛機(重量被機翼提供的升力所平衡);
(3)重返大氣層以及降落傘著陸(重量被反向的空氣阻力所對抗);
(4)太空航行器的軌道動作(此時火箭提供推力)。2、跳傘過程中的自由落體階段地球上,在真空管中下落,例如:物理學展示
重返大氣層以及降落傘著陸(重量被反向的空氣阻力所對抗)。
![自由落體[10] 自由落體[10]](/img/1/027/nBnauM3X3MTO1MzN5kzNzYTO1UTM1QDN5MjM5ADMwAjMwUzL5czLxczLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg)
