定義
眾多版本
重力是力學中最重要、最基本的概念之一。但是,國內外各種課本及參考書對重力概念的定義不盡一致,基本上是以下5類:
1.“物體由於地球的吸引而受到的力。”
2.“地球對地球表面附近物體的引力稱重力。”
3.“質點以線懸掛並相對於地球靜止時,質點所受重力的方向沿懸線且豎直向下,其大小在數值上等於質點對懸線的拉力。"
“實際上,重力就是懸線對質點拉力的平衡力。”
“物體在地球表面附近自由下落時,有一豎直方向的加速度g,產生此加速度的力稱為重力。”
4.靜止在地面上的物體,所受重力是地球對物體的萬有引力的不能產生加速度的那個分力,能產生加速度的作用效果全部分給另一個分力,即物體隨地球自轉所需要的向心力。
5.“地面附近一切物體都受到地球的吸引,由於地球的吸引而使物體受到的力叫做重力。”
以上5類定義中,第1、2、3類是在不同情況下做近似研究時使用的。第5類定義為了適應低難度的要求,只輕輕地觸動了一下重力的邊沿,讀者只能看到重力模糊不清的形象。第4類是在慣性系下建立起來的,意義雖然狹窄但是確切。
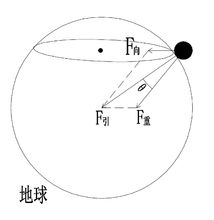 地球吸引力
地球吸引力第4類定義能揭示重力的生成所需要的兩個並列條件,一個是物體受萬有引力,另一個是物體加速運動。第4類定義可以成為諸定義的代表,在後面的敘述中稱為“重力原定義”。下面是重力原定義的示意圖,展示了重力 F萬有引力 F和向心力 F之間的關係:
需要注意的是,以上這幾類定義有著共同的缺陷 :
①只適用於地面附近這個範圍。因為定義是在地面附近建立起來的,不能隨便套用到離地面更遠的空間,更不能隨便用到宇宙空間。但是在月球、火星等外星上或飛往太空路上的飛船上,都離不開研究物體在那裡的重力。
②即使在地面附近,求物體的重力時,也只考慮了地球對物體的萬有引力和物體隨地球自轉的向心力,卻沒有考慮太陽、月亮及其他星球對物體的萬有引力還有物體隨地球繞太陽公轉的向心力等,這是不能被人接受的。
爭議
重力是所有物理量中,唯一能有眾多版本同時存留至今的物理量,這種現象不一般。這說明重力定義的確立存在相當大的困難。像萬有引力、彈力、摩擦力這些力學中的物理量,還有熱學、光學、電學、原子物理學中的各種物理量的定義都確立了單一的精準版本。
重力定義沒有一個版本能排除其他版本的存在,而在力學中獨占其位。確立重力定義的艱難使得有關重力的討論不得不被眾人遠遠地迴避。這種身邊科學比高深科學還難搞明白的現象,不符合人對自然界的認識規律。
重建原因
像萬有引力、彈力、摩擦力還有電場力、磁場力等,這些力都是客觀存在的真實力,它們的定義是在無數次實驗的基礎上建立起來的,又經過無數次實驗證明了它們的正確性。但是重力定義的建立卻沒有這些過程。重力是在已經存在的理論基礎上,經過科學思維,人為地想像出來的虛擬力。跟那些實際力定義的誕生完全不一樣。這就是重力定義多次重建的內在因素。
既然重力定義是人為想像出來的,那么重力的定義也可以人為地改變。萬有引力、彈力、摩擦力等那些真實力沒有這么隨便。
新版本
2012年在力學界出現了重力第6類定義的新版本,重力第6類定義是:在靜力學範圍內,以放置物體的支持物或物體自身為非慣性參照系,物體所受各萬有引力與各慣性力的合力叫重力。下面對新定義做深入說明:
1.物體所受來自外星球的萬有引力和與之對應的慣性力相互抵消。
以天體自身為非慣性系,在宇宙中,被看成質點的天體,或相對於天體極小的人造天體、關閉發動機的飛行器等,都是被視為質點的“天體質點”,它們在軌道上運行著。因為天體質點不受萬有引力以外的其他種類的力如支持力、發動機的推動力的約束,所以某天體所受另一天體的萬有引力會全部用來產生該天體的加速度,且對應出一個慣性力。因為此慣性力大小等於該天體的加速度大小與該天體質量的乘積,而來自另一天體的萬有引力的大小也等於這個乘積,而此慣性力的方向與此萬有引力方向相反,所以另一天體對該天體的萬有引力和與其產生的加速度對應的慣性力相互抵消。這樣來自另一天體的萬有引力全部用來產生該天體的加速度的力,就沒有使該天體獲得重量的作用效果了。
把宇宙中天體視為質點之後,物體的運動軌跡和動力學規律與所在天體相同,就有理由把物體和所在天體視為在同一軌道上運行的兩個天體。所以來自其他天體對物體的萬有引力也能和與其產生的加速度對應的慣性力相互抵消。物體沒有從來自其他天體的萬有引力那裡獲得重量。
2.物體所在星球對物體的萬有引力和與之對應的慣性力不能相互抵消
物體所在星球對物體的萬有引力,不能再和與之對應的慣性力抵消。因為所在星球表面對物體存在著支力的約束,所在星球對物體的萬有引力就不能全部用來產生物體的加速度了,只有一部分產生加速度(隨星球自轉的向心加速度),另一部分使物體獲得重量。
後面將經常遇到像第1條和第2條這樣的問題,不再詳細說明。
3.在新定義下地面上物體所受重力的矢量表達式(在其他天體上有相同的推導過程)
在新定義下以地面為非慣性系,利用力的平衡原理可以較嚴密地推導出地面上物體所受重力的矢量表達式。(統一用F代表萬有引力,f代表慣性力,G代表重力,N代表支力。黑體字母代表的是矢量,下面進行的是矢量運算)
放在支持物上的物體受到地球的萬有引力,還有太陽的萬有引力,月球的萬有引力,及其他星球的萬有引力。還有因地球自轉而存在的慣性力f地、太陽的萬有引力(使物體隨地球繞太陽公轉)對應的慣性力、月球的萬有引力對應的慣性力,及其他星球的萬有引力對應的各慣性力。還有地面的支力,等等。所有這些力相互平衡,就有:
F地+F太+F月+…+f地+f太+f月+…+N地=0
因為除地球外,太陽、月球及其他星球的萬有引力都和與之對應的慣性力相互抵消,經過整理得出 :
①-N地=F地+f地
因為地面的支力與物體受的重力G相互平衡所以有:
②-N地=G
把②式代入①式得:
③G=F地+f地
③式就是在新定義下地面物體所受重力的矢量表達式。此式表示出,物體所受重力等於地球的萬有引力和與物體隨地球自轉的向心加速度對應的慣性力的合力。
可以看出在地面附近求重力時,太陽、月球及其他星球的萬有引力不參加運算也是正確的。
4.新定義與原定義是等效的,原定義是新定義的一個特例
可以證明新定義與“在慣性系下,重力是地球對物體的萬有引力的分力,另一個分力是向心力。”這個原定義是等效的,只是新定義選用了非慣性系。
由新定義可知,地面物體所受重力的矢量表達式是 :
①G=F地+f地
慣性系下的原定義是:地球的萬有引力等於物體隨地球自轉需要的向心力和物體所受重力G的合力。其表達式是:
②F地=F向+G,此式整理後是
③G=F地-F向
因為物體隨地球自轉所需要的向心力F的大小,等於與此向心力對應的慣性力的大小,而它們的方向相反,即-F向=f地,代入③式得
G=F地+f地,此式與①式相同。
所以新定義的①式與原定義的②式是等效的。
在下面的示意圖中,還可以用幾何方法證明新定義與原定義是等效的。
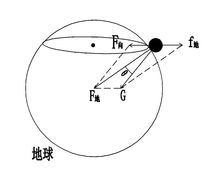 重力
重力由萬有引力、重力G、和慣性力組成的平行四邊形,是新定義的示意圖。由向心力、和G組成的平行四邊形是原定義的示意圖。可以看到在兩個平行四邊形中,慣性力與向心力大小相等方向相反,兩個萬有引力重合,兩個重力重合。證明了兩個定義是等效的。
新定義不僅適用於地球上的物體,也能廣泛地套用到宇宙中天體和人造天體及飛行器上。實際上地球也是宇宙中的天體。
新概念內涵
1.物體的加速度是決定重力大小和方向的重要因素之一。而加速度與參照系有著密切的關係,因此選擇合適的參照系,能獲得最簡便的研究重力的方法。如果參照系選擇不當,有的時候會出現錯誤的結論。(這一點與萬有引力、彈力、摩擦力這些實際的力大不相同,這些力的大小和方向與物體的加速度沒有直接關係,因此參照系的選擇不改變對它們研究的難度)本定義中選擇放置物體的支持物或物體自身為非慣性系。
2.重力是萬有引力與慣性力的合力或說它是萬有引力的一個分力,而力的合成得出的合力或力的分解得出的分力,都是人為想像出來的力。所以重力是個虛擬力。
3.地球、月球、火星、人造地球衛星等,從物理上講它們沒有本質的區別,都是名副其實的天體。根據新定義(重力是物體所受萬有引力和慣性力的合力)同一個物體放到不同的天體上,物體所受重力相差很大。比如同一個物體在月球上比在地球上重力小許多,放到人造衛星上重力就是零了(完全失重,實際上只是人造衛星對物體的萬有引力及其微小)。
4.同一物體所受重力,會因加速度的變化而發生很大變化。
5.天體間的距離遠遠大於天體的直徑,所以計算天體之間的萬有引力時可以把天體視為質點。除物體所在的天體外,其他天體對物體的萬有引力都能和與之對應的慣性力相互抵消。但是實際上,天體(除人造天體外)的體積很大。使得天體表面上物體的加速度與天體質點的加速度不同,而且隨時變化。所以物體所受其他各天體的萬有引力不能與各自對應的慣性力完全抵消了,從而使得天體表面上物體的重力發生變化。這就是地球海洋發生潮汐變化的原因。
實踐檢驗
通過下面三個實例可以檢驗新定義的科學性。
失重到“獲重”
 帶有人造重力裝置的人造天體
帶有人造重力裝置的人造天體使衛星自轉達到一定轉速,原來完全失重的太空人可以恢復類似在地面上的體重。這種想法早在二十世紀60年代,就在一些科普讀物上出現了,幻想在衛星上製造與地球表面類似的生活環境。只是當時沒有意識到,在失重狀態下長期飛行,會使骨骼脫鈣,肌肉變得鬆弛等,傷害太空人的健康。遠征火星將經過漫長的歲月,為了使健康狀況允許太空人堅持完成人類賦予的科研任務,科學家準備在載人飛船座艙中安裝“人造重力裝置”,其想法和前面是一樣的。使處於失重狀態的物體重新獲得類似地面上的重量的過程,簡稱“獲重”。獲重的基本原理可以運用重力的新定義來解釋。座艙中的太空人所受各星球的萬有引力,已經分別被各萬有引力加速度對應的慣性抵消掉。在沒有萬有引力可利用的情況下,太空人想獲得重量,只能靠慣性。這就使科學家想到,讓座艙自轉。這樣體重的獲得就沒有萬有引力參與,太空人所受重力只等於他隨座艙自轉的向心力所對應的慣性。可見“獲重”是依賴其矛盾的另一方面“失重”而存在著。
地球橢球形的成因
在慣性系下觀察,由於地球自轉,地球表面放置的物體具有向心加速度。赤道上物體的向心加速度最大,兩極上物體的向心加速度等於零,最小。
為解釋地球略顯橢球形的原因,應分別選擇物體在不同緯度上的位置為非慣性系。同一個物體在赤道上,物體的向心加速度最大,所以物體所受的慣性力最大,方向卻與萬有引力相反,而且所受萬有引力也最小。這樣一來萬有引力與慣性力的合力,相對與其他緯度就最小,也就是重力最小。在兩極上相對其他緯度萬有引力最大,而向心加速度為零即最小,慣性力也最小,所以重力最大。這樣同一物體從赤道移到極地,重力由最小逐漸變到最大,同時物體的比重也逐漸變大。海水是地球表面的主要組成部分,赤道附近的海水比重最小,根據連通器的比重小的一側液面比另一側高的原理,這裡的海面會突出一些。這就使得可塑性的地球在以這種形式分布的重力作用下,就變成赤道距地心遠,兩極距地心近的橢球形狀。
雖然海平面是橢球形,但是在地球表面任意一點上,物體受重力的方向總是垂直於所在位置處的海平面,或說總是垂直於與海平面平行的靜止水面。
潮汐的成因
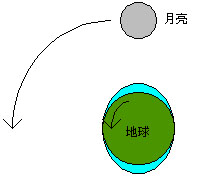 圖1
圖1潮汐的成因主要來自月球和太陽對海洋的作用。這裡只分析月球的作用。由於月球對海洋的作用,漲潮現象同時發生在地球離月球最近的海面和離月球最遠的海面這兩個區域(兩個區域中心分別稱為近月點和遠月點),
從而使橢球形的海平面疊加了紡錘體形(如圖1)。為什麼會這樣?
在敘述之前約定,忽略地月以外的其他星球的影響,並且不考慮地球自轉和公轉等分運動。潮汐現象出現紡錘體形海平面的說法,就是沒有考慮地球的自轉和公轉。
有理由認為實際情況是,地球自轉使得下面的過程隨時發生著:在近月點的地球物質離開的同時,另一部分地球物質移進近月點,並且繼承了離去的地球物質的運動狀態,遠月點也是這樣。這就保持了紡錘體的兩端總處在近月點和遠月點。
用黑體字代表矢量,統一用F代表萬有引力,f代表慣性力,用G代表重力,分別以各自的位置為非慣性系,下面的運算是矢量運算。
查看圖2,在地心處取質量為m的物質,在近月點取質量為m的物質, 在遠月點取質量為m的物質,把三份物質視為三個物體並作為三個研究對象,設定m=m=m。
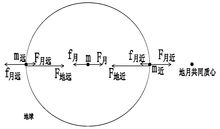 圖2
圖2把地球和月球看作質點,說是月球繞地球做圓周運動,實際上是月球和地球都繞二者的共同質心做圓周運動,只是地球的圓周軌道小得多。(雙星的兩個質量相近的星球的圓周軌道近似相等)地球質點受到月球質點的萬有引力正是地球質點繞共同質心做圓周運動的向心力,所以這裡的萬有引力等於向心力。以地心為非慣性系,此向心力對應的慣性力與此向心力大小相等方向相反。所以地球質點受月球質點的萬有引力與這個慣性力大小相等方向相反,相互抵消。
物體m在地心上,它的運動軌跡和動力學規律與地球質點的完全一樣,所以就可以把m看作與地球在同一軌道上運行的行星。這樣m受的月球的萬有引力和與之對應的慣性力相互抵消了。這裡有的關係,下面就以此式為準,比較力的大小。
實際上地球的體積很大,不能看作質點了。因為遠月點、近月點、地心、月心還有地月共同質心總是在同一直線上,所以兩點兩心繞地月共同質心運轉的角速度相同(如圖2)。
這樣一來,m與m 的角速度相同,而m繞地月共同質心的軌道半徑比m的小,這就使得近月點的m的向心加速度比地心處m的小。結果是m受的慣性力比m的小。又因為m與月球的距離也比m的小,所以m受月球的萬有引力大於m的F 。以 =為標準來對比可知大於f得出與的合力與m受地球的萬有引力反向。來求m的重力,=+(+), 可知m受的重力小於所受地球的萬有引力(若無月球的作用則=),即由於月球的作用 m所受重力變小,m的比重也變小。如果m是這裡的海水,那么這裡就會有漲潮發生,這跟上段說的連通器原理相同。用同樣的方法研究遠月點的m,雖然已是小於,但是二者的合力卻也是與地球的萬有引力反向。月球的作用也使m的重力變小,比重也變小。所以遠月點的海水同時也會有漲潮發生。這就使得海平面微微呈現出紡錘體的形狀。
太陽對海洋的作用的分析方法與月球的一樣。兩者的共同作用,再加上它們軌道平面的相互交叉及不同地區的地形地貌各異,還有地球自轉等,使得地球表面具體地點的潮汐現象變得複雜。
如果月球上有海洋,那裡也會有潮汐現象發生。因為月球半徑與月球運行軌道半徑的比值已經很小,所以現象會不太明顯。
小行星靠近木星時會有被撕裂的現象發生,也可以用這裡的方法解釋。
實驗指南
重力的大小與什麼因素有關一.實驗目的:探究重力的大小與質量的關係。
二.實驗器材:彈簧測力計、支架、相同的鉤碼5個、鉛筆、刻度尺。
三.實驗要求:
1.提出問題:重力大小可能與什麼因素有關?
2.猜想與假設:重力大小與質量有什麼關係?
3.設計並進行實驗:
(1)檢查器材:觀察彈簧秤的量程、最小刻度值,指針是否指到零刻度線。
(2)將彈簧測力計懸掛在支架上。
(3)將鉤碼逐個加掛在測力計上。
(4)將5次的測量結果記錄在表格中。
4.分析與論證:
(1)用5組數據在圖像中描點並繪出圖線。
(2)根據圖線得出結論。
6.整理器材、擺放整齊
四.實驗記錄
1.記錄數據:
物理量1234
質量m/kg
重力G/N
G/m
問題分析
衛星失重
一個是解釋衛星失重的觀點:人造衛星的向心加速度,“它的大小等於衛星所在高度處重力加速度的大小。這跟在以重力加速度下降的升降機中發生的情況類似”。
必須分析下面的問題:
不考慮地球的公轉和地球以外的其他星球的影響,在地球以外的某慣性系下進行研究。這就既能觀察到地球的自轉,更能觀察到衛星的正確運行軌道。在這個慣性系下,重力原定義認為,地球對物體的萬有引力可以分解為隨地球自轉的向心力和重力這兩個力。用這樣的思維方法進行下面的分析。(地球的萬有引力簡稱地球引力)
構想赤道上有一個與同步衛星等高的支架。第一步把一個物體放到支架底部。在支架的約束下,物體隨地球自轉而做勻速圓周運動。物體所受地球引力被分解為一個很小的向心力和一個比地球引力小不多的重力。接下來,把重物從底部逐步向上移動,先後放到支架的不同高度的位置上。在這個過程中,地球引力越來越小,分解出來的向心力越來越大,且逐漸逼近地球引力。分解出來的重力越來越小,且逐漸趨向零。最後一步,把物體移到支架的頂部。這時向心力就等於地球引力了,而重力就小到零了,物體成了一顆新的同步衛星了。它的向心力決然不等於重力,那么向心加速度能等於重力加速度嗎?顯然不能。實際上任何一顆衛星受的地球引力的作用效果只有一個,產生加速度。即全部用來提供向心力,沒有留下一點使物體獲得重量的作用效果。作用效果沒有了,重力就是零了,重力加速度也是零了。正確地說應該是:“完全失重的原因是:衛星的向心加速度的大小等於衛星所在高度處的萬有引力加速度的大小。
在解釋衛星失重的觀點中,生硬地把自由落體中的規律用到衛星上,說“這跟在以重力加速度下降的升降機中發生的情況類似” ,有似是而非的感覺。如果忽略地球自轉,萬有引力就是重力,這種近似研究就可以說成:“這跟在以萬有引力加速度下降的升降機中發生的情況類似”就正確了。
觀點中有“衛星高度處”這詞語,說明觀點本意是以地面為高度起點,並以地面為參照系,這就出現問題:一是在非近似研究(理論研究)中,以地面為非慣性系時牛頓運動定律不成立,不能研究衛星的動力學問題。二是衛星的動力學問題不屬於近似研究的範圍,也不能以地面為慣性系。所以“衛星高度處”的提法放哪兒都不適宜。必須在地球外某慣性系下才能正確地研究衛星的動力學問題,在此慣性系下衛星的動力學規律與地球的自轉沒有任何關係。可是重力這個虛擬力卻是因為地球自轉才能“存在”的,那么衛星失重的問題就與重力加速度掛不上鉤了。
用重力的新定義研究,衛星受地球的萬有引力和與之對應的慣性力相互抵消,衛星受的重力為零,但是衛星受的向心力不為零。或說重力加速度為零而向心加速度不為零,二者不可能相等。
對於正常運行的衛星來說,衛星內的物體得不到支持力,物體的重力就不可能存在,重力加速度也不存在了,但是向心加速度依然存在。從這方面看,向心加速度也不能等於衛星高度處的重力加速度。
實際上求衛星及其內部物體的重力時,是在一個非慣性系下進行的,而求它們的向心力時是在另一個慣性系下進行的, 本來兩個參照系下,運動學的量就不該對比。
宇宙飛船失重
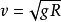 重力
重力再一個問題是解釋宇宙飛船失重的觀點:在地面附近圓周軌道上運行的宇宙飛船,設它的線速度為υ “它的軌道半徑近似等於地球半徑R,航天員受到的地球引力近似等於他在地面測得的體重mg …… 還可能受到飛船座艙對他的支持力F。引力與支持力為他提供了繞地球做勻速圓周運動所需要的向心力”。通過分析,列方程式並解出,“當
時座艙對航天員的支持力F=0,航天員處於失重狀態”。
需要思考下面的問題:
①為了得出F=0這個精確(理想化)的等式,衛星軌道半徑的值卻近似地取了地球半徑的值R,地球引力值也近似地取了地面上體重的值mg。做純粹的理論推導的過程是不能像做近似計算那樣取許多近似值。
②在這個觀點中,只用在地面附近軌道上運行的宇宙飛船說問題,沒有用任意軌道上的太空飛行器說問題,也沒進行拓展,所以沒有廣泛的意義。說明不了任意軌道上的太空飛行器都會有失重現象發生。
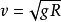 重力
重力③在觀點中,通過近似推導,得出結論 “當
時座艙對航天員的支持力F=0,航天員處於失重狀態”。這裡的“當”基本上是“條件”的意思。可是,只要是在地面附近的軌道上正常運行的太空飛行器,失重現象就會無條件地發生!
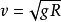 重力
重力④當等式
不成立時就有F≠0,航天員就不會失重嗎?不是,可是觀點中說的很像“是”。實際上,即使此宇宙飛船的線速度發生改變,不再是
,太空飛行器也只會改變軌道,而失重現象必定存在著,除非開啟發動機或掉到地面或其他星球上。
失重環境
還有一個問題是,認為存在著“完全失重的環境”的觀點:“繞地球做勻速圓周運動的宇宙飛船”內“航天員處於失重狀態。”“其實任何關閉了發動機,又不受阻力的飛行器的內部,都是一個完全失重的環境。例如向空中任何方向拋出的容器,其中的所有物體都處於失重狀態。”
在非慣性參照系下,物體完全失重的現象的本質,是物體所受萬有引力和與這個萬有引力產生的加速度對應的慣性力相互抵消,重力變為零,所以完全失重。物體一旦完全失重就與物體周圍的空間環境沒有任何關係,與“完全失重的環境”無關。舉例說明:
①假設宇宙飛船或拋出的容器能像貝殼一樣打開了,物體已經不在原來的“完全失重的環境”,可是物體的運動規律沒有任何變化,不是仍然處於完全失重狀態嗎?
② 在軌道上,讓大衛星在不接觸小衛星的情況下把小衛星裝進大衛星。這樣小衛星處在“完全失重的環境”,按上述觀點說小衛星完全失重。可是小衛星進入大衛星前後的運行姿態並沒有改變,所以小衛星在單獨運行時雖然沒有處在“完全失重的環境”,但是已經處在完全失重狀態。
用上述“裝入方”也能證明拋體自身一定處在完全失重的狀態。
③ 在半空中一隻長管上端的外部,用懸繩把一物體系入管內,懸繩另一端固定。然後使長管自由落下,此時管內是個“完全失重的環境”,但物體被固定著,它雖然處在“完全失重的環境”內,卻沒有失重。
④ 從放在地面上的長管上端,滴入一滴水使其自由下落,水滴呈球形,因為它處在完全失重狀態。但是水滴經過的地方不是“完全失重的環境”。
實際上宇宙飛船自身或拋出的容器自身也必然處在完全失重狀態。因為它們所受的萬有引力與對應的慣性力也相互抵消,重力也是零,當然失重。所以說,“完全失重的環境”沒有存在的意義。失重現象同時發生在物體的每一個質元上,是物體自身的事情,與所處的空間無關。
近似套用
最後一個觀點,近似方法採用的重力定義是:“地面附近一切物體都受到地球的吸引,由於地球的吸引而使物體受到的力叫做重力”。
①重力是高中力學重要的概念,重力的套用貫穿力學內容的前後。近似方法給出的重力定義,只輕輕地觸動了一下重力的邊沿,給出一個形象模糊的重力概念。帶著重力疑團進入力學,用不明性能的重力工具解決一個個力學問題,會遇到許多困難。
②在近似研究中,並沒有顯現出重力獨有的性質和重力獨到的作用。實際上是用披著重力外衣的萬有引力參加動力學的各種研究過程。雖然給出了重力的定義但是沒有真正套用它。
③從實質的角度看,在地面附近,重力本身就是帶有微小系統誤差的萬有引力,這個系統誤差是地球自轉引起的。既然如此,近似研究時引入萬有引力就可以了,只需說明測量時必然存在系統誤差,這種誤差不影響萬有引力的在地面附近的套用。這樣就可以把重力在中學教材中搶占的位置還給萬有引力。這樣一來,在中學教材中重心要改成質心,重力加速度要改成萬有引力加速度,重力勢能要改成萬有引力勢能等等。重力的難度遠大於萬有引力,在中學階段重力內容已經超出理解能力。
加速運動物體的平穩運行
下面的例子都是不計地球自轉的影響,以研究對象為非慣性系,研究對象相對於參照系靜止,這樣就可以在靜力學範圍內研究重力,這裡著重分析加速運動物體的平穩運行(不傾復)和重力的變化。設萬有引力為F,慣性力為F,重力為F。
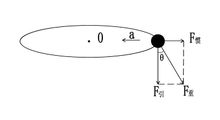
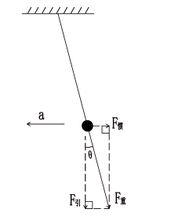
1、在靜力學範疇內,以規定的速度行駛在轉彎處的火車為非慣性系(為使拐彎時的車速與所需向心力剛好匹配,此處外側的鐵軌比內的側高出一定距離),研究車廂轉彎時的受力情況。此時車廂做勻速圓周運動,向心加速度方向指向彎道內側的圓心處,慣性力與向心加速度方向相反。車廂受到的地球萬有引力與慣性力的合力就是重力,重力與兩鐵軌支力相互平衡。從(圖1)可以看出重力不再是豎直向下,而是偏向彎道外側,偏離豎直方向一個角度θ,即與兩鐵軌所在平面垂直,使重力作用線通過兩鐵軌支撐面的中央。重力大於萬有引力,這時車廂出現超重現象。
實際套用:騎腳踏車的人在轉彎的時候,總是讓車身向彎道內側傾斜一個適當角度,從而使人和車所受合重力的作用線通過車輪下狹窄的支撐面的中央,才能平穩騎行。
 (圖1)
(圖1)實際套用:站在加速運動的汽車上的人,總是讓身體向前傾斜一個適當角度(不再是垂直地面),使重力作用線通過腳下的支撐面的中央,人才能平穩。
 (圖2)
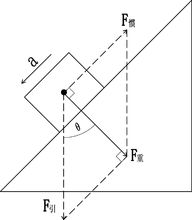
(圖2)3、在靜力學範疇內,以沿光滑的斜面 加速下滑的滑塊自身為非慣性系,研究滑塊的受力情況。滑塊相對參照系處於靜止狀態。滑塊受到的地球萬有引力與慣性力的合力就是重力,重力與斜面的支力相互平衡。平衡後,重力的方向垂直指向斜面這個支撐面(與滑塊靜止在光滑的水平面上一樣,都是垂直指向支撐面)。從可以看出,重力偏離豎直方向一個θ角,重力小於萬有引力,滑塊出現失重現象。
實際套用:加速下滑的滑雪者,必須讓身體向前傾斜一個適當角度(不是垂直於地面。如果不考慮摩擦力,應該是垂直於斜面即垂直於山坡上的雪面),使重力作用線通過腳下的支撐面的中央,才能平穩滑行。
 (圖3)
(圖3)相關內容
 重力
重力公認的理論是引力比其他的宇宙相互作用要弱得多,物理學家也一直在努力為這種說法找依據。而現在兩位物理學家Lisa Randall和Raman Sundrum則建立了另外一種模型,其中增加了額外維度和宇宙起源的追溯。
因為我們離不開地面,所以我們想當然的認為引力是一種強大的作用,其實不然。試想一下:整個地球對一根針的引力都比不過一塊小小的冰櫃磁貼,人也可以乘坐熱氣球脫離地面數小時。如果重力和原子核內質子中子之間的強力相當的話,我們早就化成一灘爛泥了。
兩位物理學家提供了這樣一個模型:構想我們所在的三維世界以及第四個維度時間都塞進了一層材料,稱為膜。這層膜漂浮在浩瀚的宇宙當中,而宇宙的其他部分並不為我們所認知。我們無法認知,是因為讓我們看到這個世界的光子沿著這層膜在爬行。而能夠影響到我們的世界,正好占據了膜的全部。
但那並不是重力。重力很小,我們又看不見,於是我們就定義這種力量為重力。在膜的作用範圍內,我們觀測到的重力比其他任何力都強。其他維度的力儘管可能與我們發生作用,但由於作用微弱,我們就像現在這樣行走於世間而不會被壓扁,地球繞著太陽公轉而沒有被太陽吸引過去,太陽圍繞銀河系中心的黑洞鏇轉而沒有被吞噬……如果能夠腦補這一切,這個模型就算出來了。
膜理論聽上去深不可測,但它也許包含了宇宙膨脹問題的答案。為什麼各種膜會彼此分離?137億年前,宇宙還是個點的時候,一切都被束縛在一起。如果膜存在,它們之間可能會有著千絲萬縷的聯繫,而在早期宇宙膨脹的時期,被吹離了彼此。
一個重力的問題,牽涉到了宇宙的未知世界。
 地球失去重力
地球失去重力重力是我們最為習以為常的事物之一。並且對於重力,我們認為下面的兩種情況理所當然:一是它自始至終就在這裡,二是它從未改變。如果地球的重力真的明顯改變,那么我們身邊幾乎所有的事物都會受到巨大的影響,因為許多事物的存在都有賴於當前的重力狀態。
在我們考慮重力變化所產生的影響之前,首先要理解什麼是重力。重力(Gravity)實際上是兩個原子之間的引力。讓我們以桌子上的兩個高爾夫球為例來說明吧!在這兩個高爾夫球的原子之間,存在著難以置信的輕微重力吸引。如果您使用兩組大量的鉛碎片和許多極為精密的工具,您可以測量出兩者之間極其微小的引力。實際上,只有當龐大數量的原子集合在一起的時候,比如我們的地球,才能產生明顯的引力作用。
地球的引力之所以恆定不變,那是因為地球的質量幾乎從未變化。要使地球重力突然變化的唯一方法,就是改變地球的質量。地球質量的變化足以引起重力變化的情況,從來不可能輕易發生。月球上的重力是地球上的6\1。
地球重力為什麼沒把我們壓碎掉?
公認的理論是引力比其他的宇宙相互作用要弱得多,物理學家也一直在努力為這種說法找依據。而現在兩位物理學家Lisa Randall和Raman Sundrum則建立了另外一種模型,其中增加了額外維度和宇宙起源的追溯。
因為我們離不開地面,所以我們想當然的認為引力是一種強大的作用,其實不然。試想一下:整個地球對一根針的引力都比不過一塊小小的冰櫃磁貼,人也可以乘坐熱氣球脫離地面數小時。如果重力和原子核內質子中子之間的強力相當的話,我們早就化成一灘爛泥了。
兩位物理學家提供了這樣一個模型:構想我們所在的三維世界以及第四個維度時間都塞進了一層材料,稱為膜。這層膜漂浮在浩瀚的宇宙當中,而宇宙的其他部分並不為我們所認知。我們無法認知,是因為讓我們看到這個世界的光子沿著這層膜在爬行。而能夠影響到我們的世界,正好占據了膜的全部。
但那並不是重力。重力很小,我們又看不見,於是我們就定義這種力量為重力。在膜的作用範圍內,我們觀測到的重力比其他任何力都強。其他維度的力儘管可能與我們發生作用,但由於作用微弱,我們就像現在這樣行走於世間而不會被壓扁,地球繞著太陽公轉而沒有被太陽吸引過去,太陽圍繞銀河系中心的黑洞鏇轉而沒有被吞噬……如果能夠腦補這一切,這個模型就算出來了。
膜理論聽上去深不可測,但它也許包含了宇宙膨脹問題的答案。為什麼各種膜會彼此分離?137億年前,宇宙還是個點的時候,一切都被束縛在一起。如果膜存在,它們之間可能會有著千絲萬縷的聯繫,而在早期宇宙膨脹的時期,被吹離了彼此。
一個重力的問題,牽涉到了宇宙的未知世界。
對地球生物
 太空中的植物呈隨機生長
太空中的植物呈隨機生長因為,有重力存在,給地球生物產生了深遠的影響。是細胞衰
老的根本原因。重力是地球上各種生物周而復始,生死循環的“罪魁禍首”。 因為有重力的作用,細胞裡面大分子,DNA和蛋白質,經過重力的長期積累,開始向某個特定的方向積累,逐漸形成細胞衰老,由於細胞衰老,從而導致生物個體死亡。
因為有重力存在,造成植物的根和莖受到重力的影響而使生長素分布不均勻,遠地側少,近地側多再有植物的不同器官對生長素的敏感程度不同,生長素濃度較高時適於莖的生長因此,植物的莖背重力生長。植物的根則具有向重力生長的特性。

